En tangent till kurvan y=sinx bildar ett område med koordinataxlarna

En tangent till kurvan $\displaystyle y=\sin x$ tangerar i punkten P, där $\displaystyle 0\le x_{p}\le \pi$ . Bestäm koordinaterna för punkten P, sådana att arean mellan koordinataxlarna och tangenten är 10 a.e.

Jag tänkte på följande vis:

Låt tangenten tangera i punkten $x=a$ . Då vet vi att tangenten har lutningen $\displaystyle k=\cos a$ samt att den då kan skrivas $\displaystyle y_{t}=x\cos a + m$ . I punkten $x=a$ delar de dessutom samma funktionsvärde, så att:

$\displaystyle\sin a = a\cos a + m \Rightarrow m=\sin a -a\cos a$

$\displaystyle\Rightarrow y_{t}=x\cos a +\sin a-a\cos a$

Jag tänkte nu att a kunde bestämmas på följande vis:

$\displaystyle \int_{0}^{(a\cos a-\sin a)/\cos a}y_{t}\;\mathrm{d}x-\int_{0}^{\pi}\sin x\;\mathrm{d}x=10$

Men löser man detta får man bara a:n som ligger utanför det givna intervallet. Ska jag då tolka detta som att det inte existerar något a i intervallet givet i uppgiften som gör att arean mellan tangenten och x-axeln blir 10 a.e?

Det som alltså avses är:

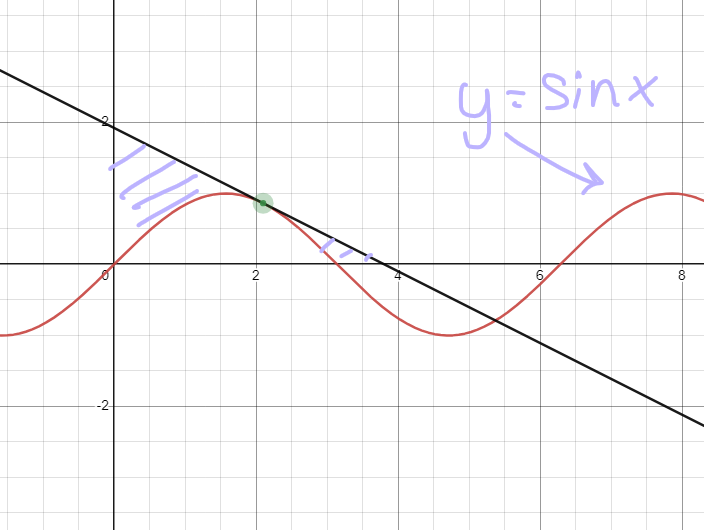
Om tangenten har ekvationen

y = kx+ m så skär tangenten y axeln vid y = m och x axeln vid x =-m/k

Arean, en triangel, 10 = - m²/(2k)

Antag att tan punkten har x = a och y = sin(a)

Lutningen i tang punkten, dvs k får du med hjälp av derivatan i punkten.

Kommer du vidare härifrån?

Jag tror du missförstod frågan lite (jag skrev den lite dumt), som du kan se i bilden är det inte hela "triangelområdet", utan bara den del där sinuskurvan inte "kommer emellan" som efterfrågas.

Om frågan är formulerad så som du skrev den, så är det du som har missförstått den. Det är triangelns area som skall vara 10 ae.

Om du menar att det är något annat som skall beräknas behöver du formulera om frågan.

Som sagt formulerade jag frågan lite dumt. Jag försökte rätta till det med en bild över vad som menades men bilden kanske inte illustrerade det ordentligt. Jag ska försöka omformulera frågan:

En tangent till kurvan $\displaystyle y=\sin x$ tangerar punkten P, där $0 \le x_{p} \le \pi$ . Bestäm koordinaterna för punkten P, sådan att arean mellan x-axeln och tangenten är 10 a.e, om man räknar bort den area som kurvan $y=\sin x$ delar med tangenten. Nedan finns en bild där området som avses är ifyllt.

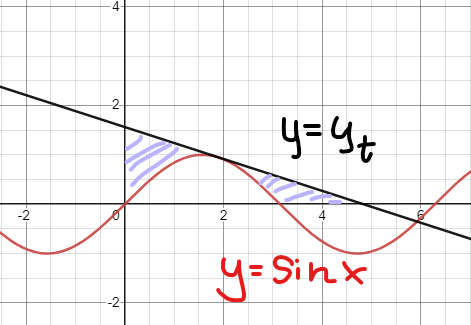
Är frågan mer förståelig nu?

Ture skrev:
Om tangenten har ekvationen

y = kx+ m så skär tangenten y axeln vid y = m och x axeln vid x =-m/k

Arean, en triangel, 10 = - m²/(2k)

Antag att tan punkten har x = a och y = sin(a)

Lutningen i tang punkten, dvs k får du med hjälp av derivatan i punkten.

Kommer du vidare härifrån?

Ok, det är en annan sak.

Då blir det lite mer komplicerat, vi måste också beakta fallet att tangenten har en positiv lutning, då hamnar arean i andra kvadranten.

Borde inte det räknas in automatiskt i min ansats? Lutningen $\cos a$ blir ju antingen negativ eller positiv beroende på vilket a vi väljer.

Det har jag inte funderat på ännu,

och hur skall vi tolka uppgiften om tangenten skär genom sinuskurvan längre bort.

ungefär så här?

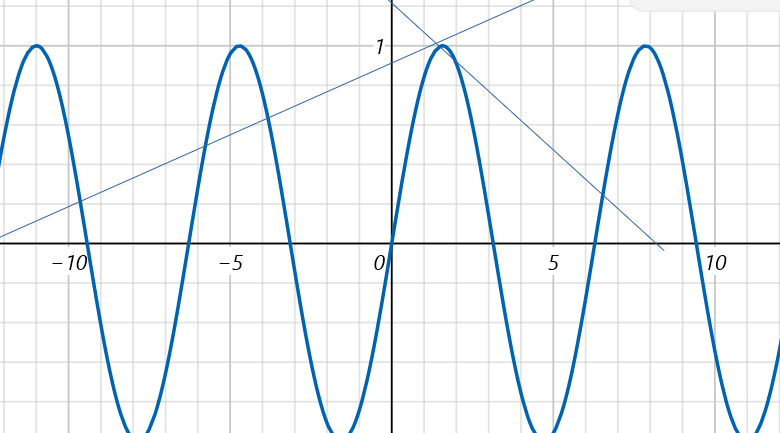
Om man betraktar den tangent med positiv lutning blir det så här då:

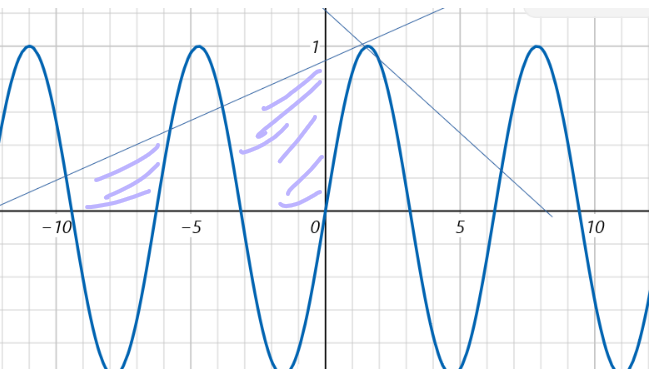
Eller nu när jag funderar inser jag att min ursprungliga ansats är felaktig. Jag ska fundera lite och återkomma!

Är det här en uppgift ur någon lärobok eller ngt du gjort själv? Och om det är ur ngn bok, är du säker på att din tolkning är korrekt?

Den är egenpåhittad.

Svara

Visa senaste svar