En inskriven fyrhörning i en cirkel

Jag testade att rita en fyrhörning med sidorna 3 och 4. Men vet inte om det finns en cirkel som går genom dess fyra hörn. Vet ni? Fick rätt svar d, iallafall. Hur skulle ni ha löst den här?
Jag tänker att en kvadrat är ett bra förstahandsval att prova. Då vet vi att det finns en cirkel så att kravet uppfylls, och det blir lätt att testa. I vissa fall måste vi kanske prova med andra alternativ, men i detta fall (och många andra) är det helt dugligt.
Smutstvätt skrev:Jag tänker att en kvadrat är ett bra förstahandsval att prova. Då vet vi att det finns en cirkel så att kravet uppfylls, och det blir lätt att testa. I vissa fall måste vi kanske prova med andra alternativ, men i detta fall (och många andra) är det helt dugligt.
Jag började med en kvadrat, gick bara att utesluta b och c då. Därför gick jag över till en rektangel
Helt rätt att prova sig fram för det allmänna resultatet = Ptomelaios sats är svår att bevisa.
Hmmm, attans, jag slarvade lite. 😅
Ett alternativ är att använda randvinkelsatsen, som för specialfallet där medelpunktsvinkeln är 180 grader ger en triangel med en rät vinkel. Vi kan därför välja exempelvis 3-4-5. Då får vi att:
vilket inte stämmer. :)
Smutstvätt skrev:Hmmm, attans, jag slarvade lite. 😅
Ett alternativ är att använda randvinkelsatsen, som för specialfallet där medelpunktsvinkeln är 180 grader ger en triangel med en rät vinkel. Vi kan därför välja exempelvis 3-4-5. Då får vi att:
vilket inte stämmer. :)
Kan du förtydliga hur du har använt randvinkelsatsen, gärna med en bild :)
Typ såhär:
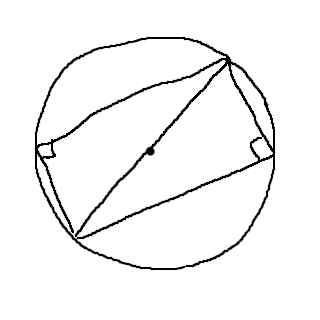
Medelpunktsvinkeln är 180 grader, vilket innebär att randvinkeln är nittio grader. :)
Smutstvätt skrev:Typ såhär:
Medelpunktsvinkeln är 180 grader, vilket innebär att randvinkeln är nittio grader. :)
jo men förstår inte riktigt vad du vill visa med det här
Din idé med en rektangel med sidorna 3 och 4 och diagonalerna 5 var väl jättebra. Det är ju lätt att inse att att den går att skriva in i en cirkel då diagonalernas skärningspunkt ligger 2,5 från varje hörn. Så är det bara att prova påståendena a,b,c,d och se att det är bara d som stämmer.
henrikus skrev:Din idé med en rektangel med sidorna 3 och 4 och diagonalerna 5 var väl jättebra. Det är ju lätt att inse att att den går att skriva in i en cirkel då diagonalernas skärningspunkt ligger 2,5 från varje hörn. Så är det bara att prova påståendena a,b,c,d och se att det är bara d som stämmer.
Varför är det lätt att inse då diagonalernas skärningspunkt ligger 2.5 från varje hörn?



