En funktion ska alltid vara växande utom i en enda punkt
Det jag inte förstår är hur kan den här alltid vara växande då K värdet på vänster sida är negativt?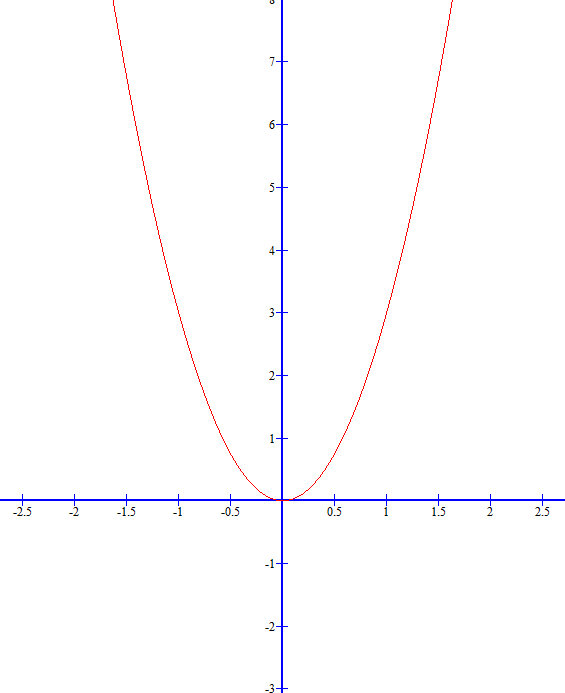
Den där funktionen är inte växande av det skäl som du pekar ut.
Dess derivata är dock växande. Kanske var det det frågan handlade om?
SeriousCephalopod skrev:Den där funktionen är inte växande av det skäl som du pekar ut.
Dess derivata är dock växande. Kanske var det det frågan handlade om?
Här är hela frågan:
För en funktion gäller: Den är alltid växande, utom i en enda punkt (dvs en
terrasspunkt). Rita hur grafen till funktionens derivata kan se ut!
Blir så förvirrad
En funktion som är växande hela tiden ser ju ut ungefär så här: /. En funktion som är växande utom i en punkt ser ut så här/ och så lutar den mindre och mindre ända tills den inte lutar alls, och sedan lutar den mer och mer tills den ser ut ungefär så här igen: /. Derivatan av denna funktion är först positiv, sedan blir den mindre och mindre (men fortfarande positiv) tills derivatan blir 0 och sedan blir derivatan större och större. Jämför detta med din bild! Bilden skall ju föreställa derivatan, inte själva funktionen.



