En fråga gällande additionsmetoden

De måste inte stå under varandra, men de termer du vill eliminera måste ha rätt tecken för att de ska kunna "ta ut" varandra. Det har de inte i ditt fall, varken innan eller efter att du subtraherade 6y från båda sidor.

Kontrollera:

Om ena ekvationen är 8x = 14-6y och andra ekvationen är 9x+6y = 3 så får du efter additionen:

(8x)+(9x+6y) = (14-6y)+(3), dvs

17x+6y = 17-6y

Här sitter du fast.

=========

Du kan istället göra så här:

Skriv första ekvationen som 14-6y = 8x och andra ekvationen som 9x+6y = 3.

Då får du efter additionen:

(14-6y)+(9x+6y) = (8x)+(3), dvs

14+9x = 8x+3

Härifrån kan du gå vidare.

=========

Eller så här:

Första ekvationen är 8x+6y = 14, andra ekvationen är 9x+6y = 3.

Om du nu subtraherar den första ekvationen från den andra så får du:

(9x+6y)-(8x+6y) = (3)-(14), dvs

9x+6y-8x-6y = -11, dvs

17x = -11

Härifrån kan du gå vidare 

Okej tack, men fråga, 

Hur får jag 8x+6y=14 att skrivas om till 14-6y=8x så där i VL och HL

ex:
8x+6y=14 (jag vill ju ha ett -6y så då måste jag flytta lite)
8x+6y-6y=14-6y
8x=14-6y (liksom då blir de ju så här att jag vidare får ut 17x=17 och jag fastnar)

sen undrar jag också hur man vet att man har fastnat, alltså undrar liksom hur vet man att x inte ska bli = 1 eller 0 (vet inte om de är en dum fråga, men frågar ändå) 

Elgib skrev:

Okej tack, men fråga, 

Hur får jag 8x+6y=14 att skrivas om till 14-6y=8x så där i VL och HL

ex:
8x+6y=14 (jag vill ju ha ett -6y så då måste jag flytta lite)
8x+6y-6y=14-6y
8x=14-6y (liksom då blir de ju så här att jag vidare får ut 17x=17 och jag fastnar)

Sedan har Yngve bara bytt plats på HL och VL. Nu har han tagit fram två ekvationer med +6y i den ena och -6y i den andra, så när man adderar de båda ekvationerna blir man av med alla y, och har bara kvar en ekvation med EN obekant, nämligen x, och sådana kan du redan lösa, eller hur?

sen undrar jag också hur man vet att man har fastnat, alltså undrar liksom hur vet man att x inte ska bli = 1 eller 0 (vet inte om de är en dum fråga, men frågar ändå) 

Om du (av någon anledning) tror att x skall ha värdet 0 så kan du sätta in x i den ena ekvationen, räkna ut y, sätta in detta värde och x = 0 i den andra ekvationen och kolla om det stämmer - i så fall har du hittat en lösning. Men man behöver nog ganska mycket tur för att råka gissa rätt...

Jo men att lösa de, ska nog inte vara svårt. Men undrar mer hur de kommer sig att jag kan flytta över exempelvis 8x från VL till HL och 14 från HL till VL utan att "räkna dit dom" ? liksom hur ska jag visa min lärare de i uträkningen. Visst kan jag flytta över termerna så men då blir de ju -. ?

Elgib skrev:

Jo men att lösa de, ska nog inte vara svårt. Men undrar mer hur de kommer sig att jag kan flytta över exempelvis 8x från VL till HL och 14 från HL till VL utan att "räkna dit dom" ? liksom hur ska jag visa min lärare de i uträkningen. Visst kan jag flytta över termerna så men då blir de ju -. ?

Menar du att man hoppar över mittenraden som du har skrivit här:

ex:
8x+6y=14 (jag vill ju ha ett -6y så då måste jag flytta lite)
8x+6y-6y=14-6y
8x=14-6y (liksom då blir de ju så här att jag vidare får ut 17x=17 och jag fastnar)

Det kan man göra, när man blir van.

Om du menar något annat, så behöver du vara tydligare med vad det är du undrar över.

precis de jag menar. Hur kan jag göra så med uträkning? går det?

Du kan hoppa över mellansteget när du är så säker på det att du sällan eller aldrig gör fel i det skedet.

På Matte 2-nivå behöver du inte ta med det mellansteget i din uträkning, men det finns flera goda skäl till att göra det ändå.

===============

Dvs du kan lika gärna skriva

8x+6y = 14 ger 8x = 14-6y

som

8x+6y = 14 ger 8x+6y-6y = 14-6y, som ger 8x = 14-6y.

==============

Var det svar på din fråga?

okej, men om jag gör den omskrivningen så får jag fel, dvs om jag gör så här:  8x+6y=14      8x+6y-6y=14-6y         8x=14-6y

och sen tar:  

8x=14-6y
9x+6y=3

så får jag:  17x=17 och att x = 1 (det är fel, facit vill ha -11 på X)

Så de är för att ditt sätt är rätt och mitt är fel, men jag förstår inte riktigt hur jag kan få den ekvationen du fick fram genom att "räkna mig till det" genom balansmetoden alltså. Eller om de finns ett annat vis att räkna sig till ett rätt svar, för 1 och -11 är jätte långt ifrån varandra, så jag typ räknar rätt men räknar ändå helt fel..

Elgib skrev:

okej, men om jag gör den omskrivningen så får jag fel, dvs om jag gör så här:  8x+6y=14      8x+6y-6y=14-6y         8x=14-6y

och sen tar:  

8x=14-6y
9x+6y=3

så får jag:  17x=17 och att x = 1 (det är fel, facit vill ha -11 på X)

Du borde få 17x+6y = 17-6y som inte hjälper dig vidare. Du har tappat bort "6y" på båda sidorna (med olika tecken). Ett sätt att få det att stämma är att se till att ha "samma sorts termer" ovanför varandra, men det är inte nödvändigt.

Så de är för att ditt sätt är rätt och mitt är fel, men jag förstår inte riktigt hur jag kan få den ekvationen du fick fram genom att "räkna mig till det" genom balansmetoden alltså. Eller om de finns ett annat vis att räkna sig till ett rätt svar, för 1 och -11 är jätte långt ifrån varandra, så jag typ räknar rätt men räknar ändå helt fel..

Om i fortsätter från ekvationerna

8x=14-6y
9x+6y=3

så kan du ta första ekvationen minus andra ekvationen, term fö rterm. Då får du 8x-(9x+6y) = 14-6y-3 som kan förenklas till -x-6y = 11-6y, och om du adderar 6y på båda sidor får du -x = 11 som är samma sak som x = -11.

Elgib skrev:

Så de är för att ditt sätt är rätt och mitt är fel, men jag förstår inte riktigt hur jag kan få den ekvationen du fick fram genom att "räkna mig till det" genom balansmetoden alltså. 

Är du med på att a = b innebär att b = a?

De två ekvationerna säger exakt samma sak. Inga mystiska trollspön, bara att vi vänder på likheten.

Är du med på att 8x = 14-6y innebär att 14-6y = 8x?

De två ekvationerna säger exakt samma sak. Inga mystiska trollspön här heller, bara att vi vänder på likheten.

Nu kan du addera ekvationen 14-6y = 8x med ekvationen 9x+6y = 3 och därmed uppnå det önskade resultatet, nämligen att den obekanta storheten y elimineras.

jag förstår det där, men… 

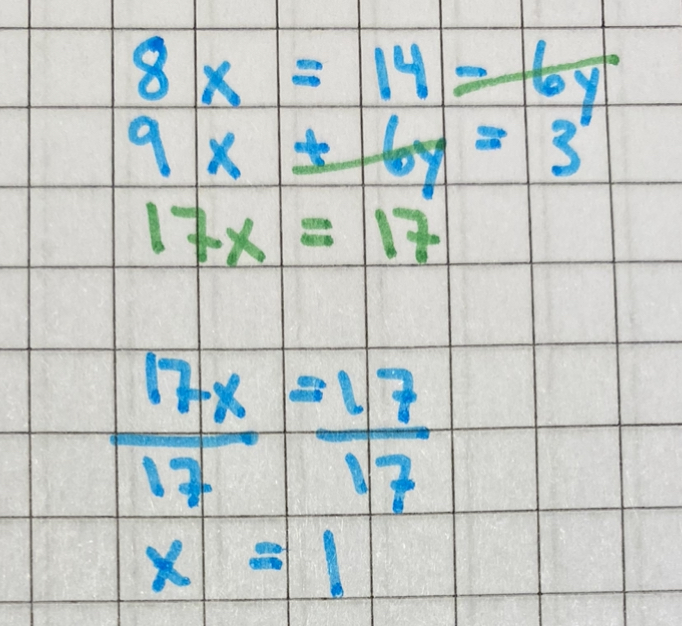
Det blir fel när du stryker -6y från högerledet i första ekvationen samtidigt som du stryker 6y från vänsterledet i andra ekvationen.

Vilken räkneoperation låter dig göra det?

Om du vill få bort -6y från högerledet i första ekvationen så måste du addera 6y till båda sidor och ekvationen blir då 8x+6y = 14.

Om du vill få bort 6y från vänsterledet i andra ekvationen så måste du subtrahera 6y från båda sidor och ekvationen blir då 9x = 3-6y.

Och då är du i stort sett tillbaka där du började.

=========== Gör istället så här =========

Gör istället antingen så att du vänder på en av ekvationerna och adderar dem (som jag tipsade om i svar #2 och svar #11) eller att du behåller ursprungsekvationerna och subtraherar den ena ekvationen från den andra (som jag tipsade om i svar #2 och som Smaragdalena tipsade om i svar #10).

okej, men jag har ekvationssystemet. 
4x+3y=7
3x+2y=1

Jag måste lösa detta genom additionsmetoden. Men för att kunna eliminera exempelvis y (som jag då tänker att jag vill) då måste jag få y termerna lika och med olika tecken (+ -) så jag skrev om de så jag fick fram: 

8x+6y=14
9x+6y=3 

Så när jag var här så undra jag om jag måste ha termerna under varandra för att kunna räkna ut det.
Alltså för att kunna addera:

8x med 9x och vidare 14 med 3 och sen (efter att jag skrivit om en ekvation så jag får -6y i den) ta -6y med +6y som då blir 0. Jag vill ta bort 6y i båda ekvationerna med hjälp av additionsmetoden. Men för att kunna ta bort 6y måste en av 6y vara negativ, så de va därför jag strök så där som jag gjorde 

Elgib skrev:

Men för att kunna eliminera exempelvis y (som jag då tänker att jag vill) då måste jag få y termerna lika och med olika tecken (+ -) så jag skrev om de så jag fick fram: 

8x+6y=14
9x+6y=3 

Det jag har markerat med fetstil är bra!

Multiplicera nu den andra ekvationen med -1.

Ekvationssystemet ser då ut så här:

8x+6y = 14

-9x-6y = -3

Nu kan du addera ekvationerna ledvis och du får då ekvationen

(8x+6y)+(-9x-6y) = (14)+(-3)

Förenklat blir det

-x = 11

Det gäller alltså, som du mycket riktigt skrev, att få t.ex. y-termerna lika stora men med olika tecken (på samma sida av likhetstecknet).

De där va ju jätte smart!! alltså de där med att multiplicera med -1. Tänkte inte alls på de. Tack för all hjälp. Fick ut rätt X värde och Y värde nu. Jätte tack!! 

Elgib skrev:

Så när jag var här så undra jag om jag måste ha termerna under varandra för att kunna räkna ut det.
Alltså för att kunna addera:

De termer du vill eliminera måste vara skrivna på ett sådant sätt att de tar ut varandra när du adderar ekvationerna ledvis.

Eftersom du summerar ena ekvationens hela vänsterled med andra ekvationens hela vänsterled och ena ekvationens hela högerled med andra ekvationens hela högerled så måste du se till att de termer du vill eliminera antingen är skrivna så att de elimineras på en gång eller att de kan elimineras i nästa steg.

===========

Om termerna är lika stora fast med olika tecken så måste de finnas på samma sida av likhetstecknet. De kan då elimineras på en gång.

Exempel:

x+y = 2

x-y = 3

Efter addition: 2x = 5

===========

Om termerna är lika stora och har samma tecken så måste de finnas på olika sidor av likhetstecknet. De kan då elimineras i nästa steg.

Exempel:

x+y = 2

x = 3+y

Efter addition: 2x+y = 5+y

Subtrahera y från båda sidor: 2x = 5

=============

Blev det tydligt då?

Elgib skrev:

De där va ju jätte smart!! alltså de där med att multiplicera med -1. Tänkte inte alls på de. Tack för all hjälp. Fick ut rätt X värde och Y värde nu. Jätte tack!! 

Ajdå, ojdå.

Det är en standardmetod för att förbereda ekvationer för additionsmetoden.

Slarvigt av mig att inte tipsa om det på en gång.

Jag är glad ändå, fick ut rätt svar och vet att jag kan använda mig av de där tricket sen i fortsättningen (om jag kommer ihåg det). Jag gjorde typ så här: 

Hade ju: 
4x+3y=7
3x+2y=1

Sen skrev jag om de genom att multiplicera första ekvationen med 2 och den andra ekvationen med 3. Då fick jag lika y termer:
8x+6y=14
9x+6y=3

Sen använde jag mig av tricket på en av ekvationerna. Multiplicera första ekvationens termer med -1 och fick då: 
-8x-6y=-14

Sen  gjorde jag bara så här: 
-8x-6y=-14
9x+6y=3
x 0 =-11
x=-11

Vidare räkna jag fram y genom att placera in -11 i en av ekvationernas x värde och fick ut att y är 17. 

Elgib skrev:

Jag är glad ändå, 

Bra.

Vidare räkna jag fram y genom att placera in -11 i en av ekvationernas x värde och fick ut att y är 17. 

Snyggt. Men du glömmer väl inte att kontrollera ditt svar?

Jag kolla bara facit. Men gjorde en kontroll på pappret nu, : ) 

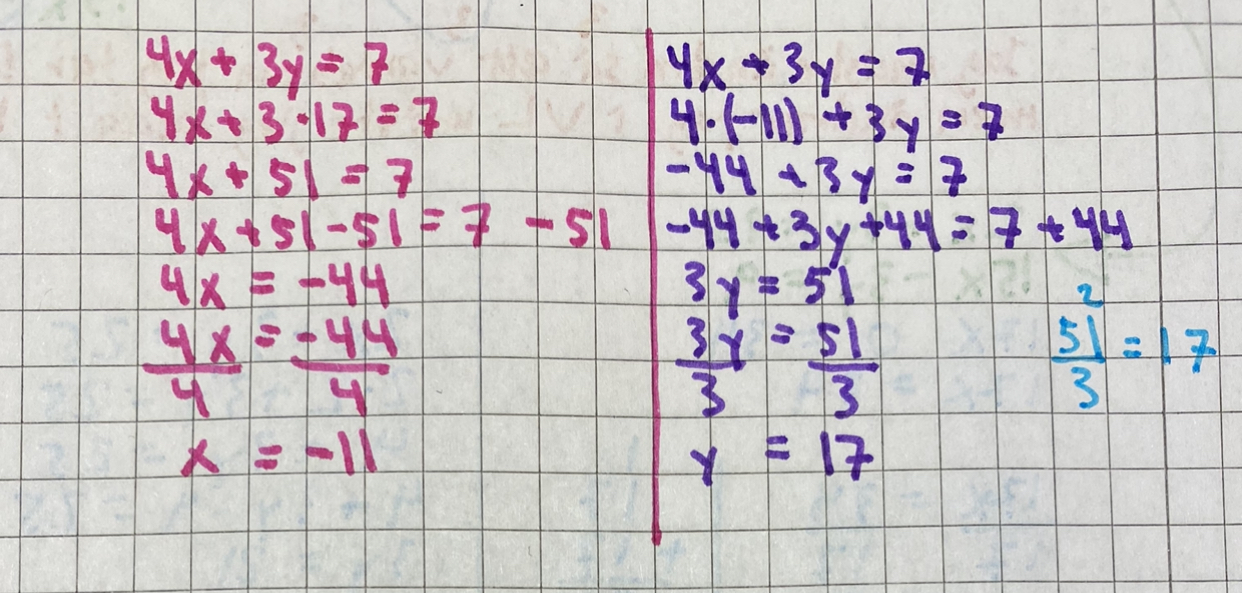
Du har bara kollat den ena ekvationen. Du bör kolla båda.

Men ett enklare sätt att kontrollera är att helt enkelt sätta in värdet för x och värdet för y i den första ekvationen och se att den stämmer.

Gör sedan samma sak med den andra ekvationen.

Jättebra tack