En bil med släpvagn
En bil med släpvagn kör genom en kurva. Kurvan har radien 80m. På vagnen finns en stor vattendunk som väger 20kg. Friktionskraften mellan vagnsflaket och dunken kan högst bli 20% av dunkens tyngd. Vilken är den högsta fart bilen kan hålla genom kurvan utan att vattendunken börjar glida?
Jag vet inte riktigt hur jag ska göra några tips?
Börja med att rita en bild på dunken med tre krafter, en tyngdkraft, en normalkraft och en friktionskraft.
Och så ett tips, för att objekt ska accelereras runt en cirkelbana (t.ex. med hastigheten och radien ) måste objektet utsättas för en resulterande centripetalkraft
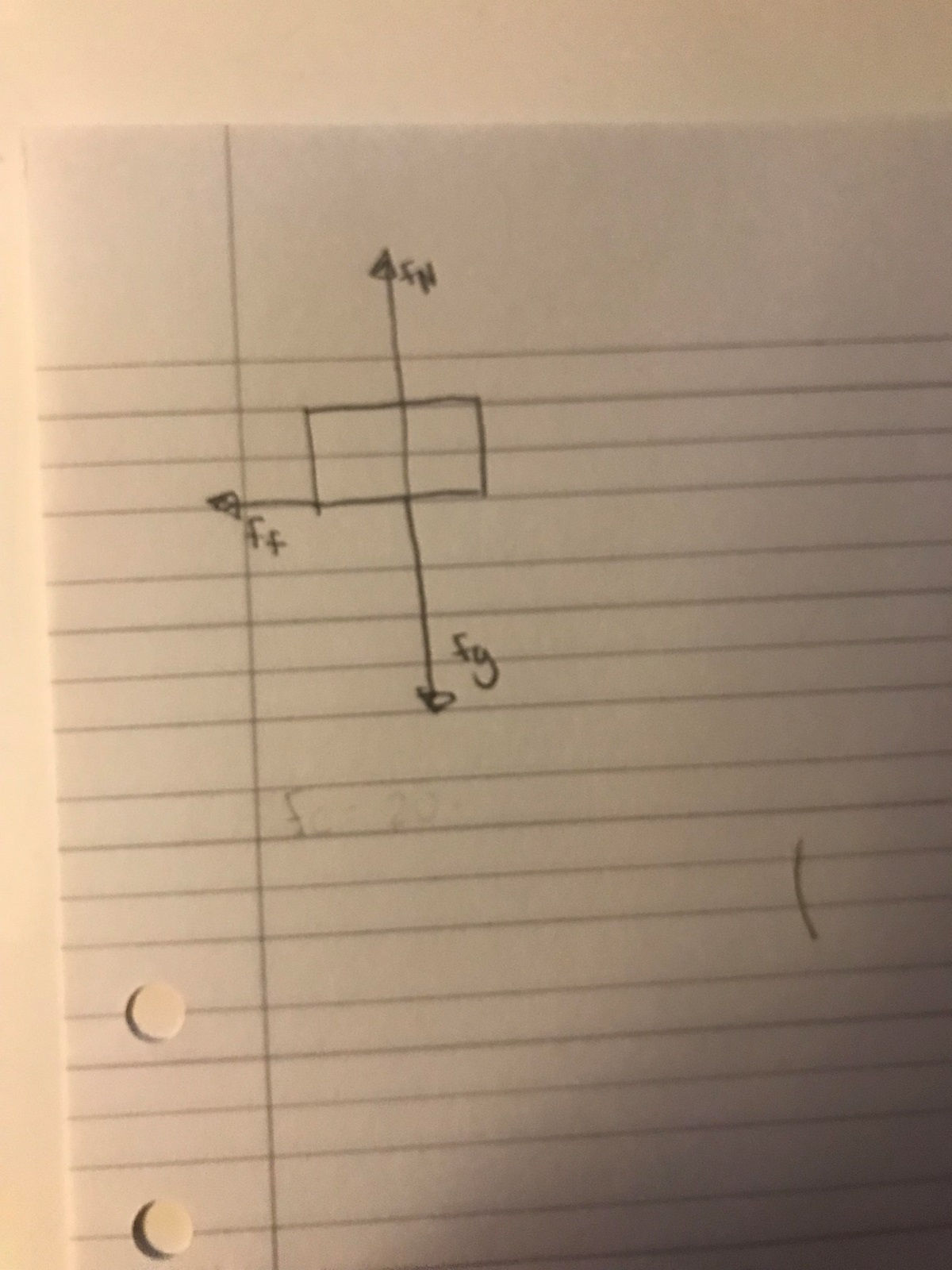
Jag kan väl inte räkna ut Fc då jag inte har v?
fg blir då 196,4n
Bra, hur stor kan maximalt bli enligt uppgiftstexten? Det är en viss procent av !
Centripetalkraften utgörs ju av , det är den enda kraft som pekar mot kurvans mittpunkt. Så
Nu kan du beräkna hastigheten
Ff kan maximalt bli 157,12N?
Ahaaa sen kan man bara räkna med fc=mv2/2 för att få v?
Ja, men 20% av är inte utan?
Fc=39,28?
japp, så v blir alltså?
12,586m/s?
Ja, fast svara med två, max tre gällande siffror. Och om man räknar utan avrundning hela vägen blir det 12.53475169...
Tack så hemskt MYCKET!!

