En behållare av en rät kon

Varifrån kommer: r=h?

Principen här är: $\frac{dV}{dt}=\frac{dV}{dh}\times \frac{dh}{dt}$

V = $\frac{{\mathrm{\pi r}}^2\mathrm{h}}{3}$

I uppgiftens text står att V = 0,64$h^3$

Varifrån kommer sambandet r = h?

jag tänkte att höjden är lika stor som radien men det är ju helt fel 

Katarina149 skrev:

Hur kommer jag vidare med min uträkning?

Här ser du sambandet mellan höjd och radie. Det kan man använda i volymformeln.

Jag förstår inte hur jag ska skriva ett samband 

i a) kan du använda V = 0,64$h^3$för att beräkna hastigheten i nivåhöjningen när höjden är 3,0 dm.

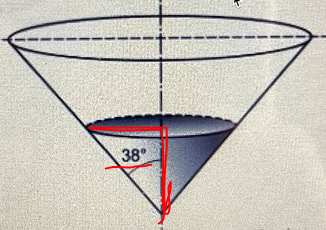
I b) ska man visa hur Anna kommit fram till sambandet. Använd då trigonometri. Vinkeln är 38 grader och x-axeln h, då kan du hitta ett uttryck för radien.

Sten skrev:

i a) kan du använda V = 0,64$h^3$för att beräkna hastigheten i nivåhöjningen när höjden är 3,0 dm.

I b) ska man visa hur Anna kommit fram till sambandet. Använd då trigonometri. Vinkeln är 38 grader och x-axeln h, då kan du hitta ett uttryck för radien.

Hur kan man i a uppgiften använda V=0.64h³ för att beräkna hastigheten när höjden är 3,0dm

Vi har:

$\frac{dV}{dt}=\frac{dV}{dh}\times \frac{dh}{dt}$

$\frac{dV}{dt}=15$

V(h) = 0,64$h^3$

$\frac{dV}{dh}$ = 3* 0,64$h^2$

Vattennivåns höjd = 3,0

15 = 3*0,64${(3,0)}^2$$\times \frac{dh}{dt}$

$\frac{dh}{dt} = \frac{15}{3*0,64{(3,0)}^2}$= 0,87

Hoppas jag räknat rätt, då blir svaret att höjden i behållaren stiger med 0,87 l/min när vattennivån är 3,0 dm.

Vad för samband bör jag kunna av vinkeln 38 grader? Är det radien jag ska räkna ut aha höjden och vinkeln 38 grader?

Jag förstår inte hur du har räknat. Men så här tänker jag 

Är det a eller b du undrar över? Stens uträkning av a) i #11 känns komplett.

b) i spoliern

Programmeraren skrev:

Är det a eller b du undrar över? Stens uträkning av a) i #11 känns komplett.

b) i spoliern

Visa spoiler

Visa V=0,64h^3

För kon gäller att:
V=Ah/3=pi*r^2*h/3
tan38=r/h --> r=h*tan38

Sätt ihop:
V=pi*r^2*h/3=pi*(h*tan38)^2*h/3=0,64h^3

Jag vill kunna utföra hela beräkningen från början men jag vet inte hur jag ska göra. Vad gör jag fel i min uträkning?

#11 är tydligt tycker jag.

r och h har ett beroende. I #13 använder du inte den givna formeln utan den generella för volymen av en kon.
Du deriverar med avséende på h men deriverar isället r. Det är fel. Men det hade varit fel även om du dervierat med avséende på r eftersom h är en funktion av r (och vice versa). Ingen av dem är en konstant.

Tänk efter vd du gör. Du delar upp: dV/dt = dV/dh * dh/dt, det är rätt. Tänk igenom vad varje del står för.
I uppgiften är dV/dt given. dh/dt söks. dV/dh är det som måste tas fram.

V(h)=0,64h^3
Det är en funktion för volymen som bara beror av höjden. Då är det enkelt att derivera och få fram V'(h).
Dessutom vet vi att h=3. Då sätter vi in det och får ekvationen:

15=V'(3)*dh/dt

I frågan har Anna beräknat volymen till V = $0,64h^3$, så då kan man använda detta för att beräkna $\frac{dV}{dh}$

Men din fråga gäller väl framför allt b), hur Anna kommit fram till det uttrycket för volymen.

Volymen för en kon är V = $\frac{{\mathrm{\pi r}}^2\mathrm{h}}{3}$, och förhållandet mellan h och r är detta:

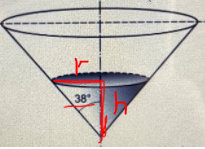
$\frac{r}{h}= \tan \left(38\right)$, vilket ger att r = h*tan(38).
tan(38) = 0,781

Då kan man skriva om formeln för volymen:

V=$\frac{\mathrm{\pi }{(\mathrm{h}*0781)}^2\mathrm{h}}{3} = \frac{{\mathrm{\pi h}}^3*0,{781}^2}{3} = \frac{0,610*{\mathrm{\pi h}}^3}{3} = 0,639h^3$

Derivera V med avseende på h, använd gärna det andra uttrycket av V ovan, så får du fram $\frac{dV}{dh}$

Och frågan gällde vattennivåns höjning när h=3,0 dm

I uppgiften används dm för längd och liter ("kubikdecimeter") för volym, så man slipper att omvandla mått.

Jag tycker att ni går fram alldeles för snabbt. Det är enbart så långt jag har lyckats förstå 

Nu förstår jag hur man ska tänka i a. Man ska alltså inte använda den generella formeln utan den formeln som anges i uppgiften. Så löste jag den . Men hur gör man i b?

Är det rätt att tänka så här i b?

I a) är det viktigt att förstå varför du INTE kan derivera som du gjorde tidigare. Beskrivet ovan.

EDIT: b) Nej, det är ren förenkling. Du ska ersätta r med h i formeln. Det finns ingen höjd 3 i formeln, höjden är h.

I a så förstår jag inte vad du menar ”med det viktigt att förstå varför du INTE kan derivera som du gjorde tidigare” . Vad menar du? 

I b hur menar du med ren förenkling 

a) Tydligt beskrivet i inlägg #16

b) Varför sätter du in h=3? Du har en formel för en kons volym. Du har fått en vinkel som gör att du kan uttrycka r som en funktion av h. Sen är det bara förenkling. Se spoiler i #14

I b får jag det till att bli som ovan. Varför blir det fel?

Det verkar som räknaren är inställd på radianer, i stället för grader.

Okej nu blev det rätt. När jag ställde in räknaren på grader blev det rätt . Tack för hjälpen!