Elkrets opamps (del 2)
Hej,
I den här uppgiften ska jag beräkna .
Jag har kommit fram till:
men jag undrar hur man tar reda på ?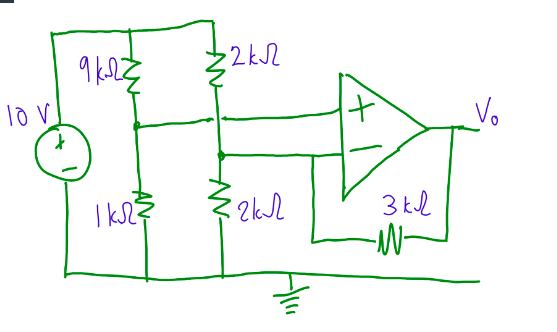
OP-förstärkaren gör allt den kan för att få lika med .
Ja, det förstår jag. Men hur ska man räkna ut i sådana fall?
Leona11 skrev:Ja, det förstår jag. Men hur ska man räkna ut i sådana fall?
Huvudräkning borde funka.
Visa spoiler
Hur stor är strömmen genom 1 kΩ-motståndet?
v+ = (1/(1+9))•10 = 1V
Jan Ragnar skrev:v+ = (1/(1+9))•10 = 1V
Varför är det just spänningen över 1k
resistorn som avgör ?
Det är en helt vanlig spänningsdelning mellan 9- och 1kohms motstånden. In-impedansen på +ingången är oändlig om vi räknar med en ideal OP.
Leona11 skrev:Jan Ragnar skrev:v+ = (1/(1+9))•10 = 1V
Varför är det just spänningen över 1k resistorn som avgör ?
Eftersom 1kΩ-motståndet är jordat på dess andra sida.
2k-motståndet är också jordat på dess andra sida så varför kan inte spänningsdelning användas på de två 2kΩ-motstånden?
Leona11 skrev:2k-motståndet är också jordat på dess andra sida så varför kan inte spänningsdelning användas på de två 2kΩ-motstånden?
Eftersom OP-förstärkarens utgångsspänning vill göra lika med .
Du skrev att du visste det men jag skriver det igen.
Är du medveten om att OP-förstärkaren underförstått också har anslutningar för matningsströmmar? Som op-förstärkaren bland annat använder för att styra strömmar in i och ut ur förstärkarens utgång?
Vid spänningsdelning måste det gå samma ström genom de två motstånden som ”delar” spänningen.
I din krets går det 4,5 mA genom det övre 2 kΩ motståndet, medan det går 0,5 mA genom det nedre och resterande 4 mA går till 3 kΩ motståndet.
Jan Ragnar skrev:Vid spänningsdelning måste det gå samma ström genom de två motstånden som ”delar” spänningen.
I din krets går det 4,5 mA genom det övre 2 kΩ motståndet, medan det går 0,5 mA genom det nedre och resterande 4 mA går till 3 kΩ motståndet.
Nu förstår jag. Stort tack för hjälpen!




