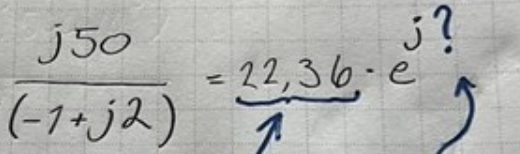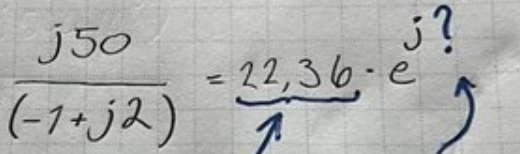Elektroteknik - Impedans
Hej! Jag har fastnat på en gammal tentauppgift och skulle uppskatta om någon kan förklara lösningsförslaget.
Det är den första biten där man ska beräkna i(t) jag fastnade på. Jag förstår inte riktigt hur vi går ifrån Z=1/j1000*20*10^(-6)+ … osv till det slutgiltiga Z=22,4*e^(-j26,6°).
Formeln för Z som står ovanför förstår jag dock.
Tacksam för all hjälp!


Testa att förlänga bråken med nämnarens komplexa konjugat, så att nämnarna blir reella. Skriv sedan om mha Eulers formel.
Kommer du vidare?
JohanF skrev:Testa att förlänga bråken med nämnarens komplexa konjugat, så att nämnarna blir reella. Skriv sedan om mha Eulers formel.
Kommer du vidare?
Tack!
Jag förstår inte riktigt. Är det så här du menar?
Jag får ut 22,4 men vinkeln -26,6° vet jag inte hur de får ut.

advodis skrev:JohanF skrev:Testa att förlänga bråken med nämnarens komplexa konjugat, så att nämnarna blir reella. Skriv sedan om mha Eulers formel.
Kommer du vidare?
Tack!
Jag förstår inte riktigt. Är det så här du menar?Jag får ut 22,4 men vinkeln -26,6° vet jag inte hur de får ut.
Bra så långt! Du har kommit fram till att den komplexa impedansen är
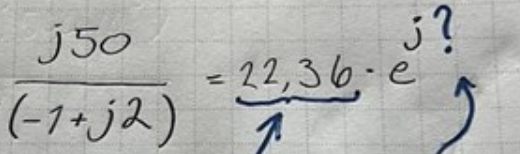
... och du har upptäckt att det är svårt att se impedansens fasvridning om den är skriven på rektangulär form, med komplexa tal både i täljare och nämnare. Det finns flera vägar att nå fram till ditt frågetecken. I min första kommentar tyckte jag att du skulle förlänga det komplexa bråket med nämnarens komplexa konjugat, dvs , och sedan kan du enkelt identifiera termer med Eulers formel, .
Alternativt kan du använda Eulers formel direkt på både täljare och nämnare var för sig, och sedan använda räkneregel för potenser,
Den senare metoden har du redan börjat använda för att beräkna absolutbeloppet, så fortsätt på den. Och med ovanstående tips kanske du nu ser hur du måste beräkna vinkeln när du har ett bråk med komplexa tal.
Hänger du med?
(edit, jag gjorde ett typo på komplexa konjugatet, hoppas du såg det)
JohanF skrev:advodis skrev:JohanF skrev:Testa att förlänga bråken med nämnarens komplexa konjugat, så att nämnarna blir reella. Skriv sedan om mha Eulers formel.
Kommer du vidare?
Tack!
Jag förstår inte riktigt. Är det så här du menar?Jag får ut 22,4 men vinkeln -26,6° vet jag inte hur de får ut.
Bra så långt! Du har kommit fram till att den komplexa impedansen är
... och du har upptäckt att det är svårt att se impedansens fasvridning om den är skriven på rektangulär form, med komplexa tal både i täljare och nämnare. Det finns flera vägar att nå fram till ditt frågetecken. I min första kommentar tyckte jag att du skulle förlänga det komplexa bråket med nämnarens komplexa konjugat, dvs , och sedan kan du enkelt identifiera termer med Eulers formel, .
Alternativt kan du använda Eulers formel direkt på både täljare och nämnare var för sig, och sedan använda räkneregel för potenser,
Den senare metoden har du redan börjat använda för att beräkna absolutbeloppet, så fortsätt på den. Och med ovanstående tips kanske du nu ser hur du måste beräkna vinkeln när du har ett bråk med komplexa tal.
Hänger du med?
 Ja nu fick jag ut det! Tack så mycket för hjälpen. Något jag inte hänger med på dock är varför det inte gick att få fram vinkeln direkt med j50/(-1+j2)
Ja nu fick jag ut det! Tack så mycket för hjälpen. Något jag inte hänger med på dock är varför det inte gick att få fram vinkeln direkt med j50/(-1+j2)
Jag editerade min kommentar lite, det hade smugit sig in ett typo...)
Som svar på min egna tidigare fråga, kan det vara för att man behöver ha två termer, a & b, som i formeln för komplexa tal för att beräkna svaret?
advodis skrev:JohanF skrev:advodis skrev:JohanF skrev:Testa att förlänga bråken med nämnarens komplexa konjugat, så att nämnarna blir reella. Skriv sedan om mha Eulers formel.
Kommer du vidare?
Tack!
Jag förstår inte riktigt. Är det så här du menar?Jag får ut 22,4 men vinkeln -26,6° vet jag inte hur de får ut.
Bra så långt! Du har kommit fram till att den komplexa impedansen är
... och du har upptäckt att det är svårt att se impedansens fasvridning om den är skriven på rektangulär form, med komplexa tal både i täljare och nämnare. Det finns flera vägar att nå fram till ditt frågetecken. I min första kommentar tyckte jag att du skulle förlänga det komplexa bråket med nämnarens komplexa konjugat, dvs , och sedan kan du enkelt identifiera termer med Eulers formel, .
Alternativt kan du använda Eulers formel direkt på både täljare och nämnare var för sig, och sedan använda räkneregel för potenser,
Den senare metoden har du redan börjat använda för att beräkna absolutbeloppet, så fortsätt på den. Och med ovanstående tips kanske du nu ser hur du måste beräkna vinkeln när du har ett bråk med komplexa tal.
Hänger du med?
Ja nu fick jag ut det! Tack så mycket för hjälpen. Något jag inte hänger med på dock är varför det inte gick att få fram vinkeln direkt med j50/(-1+j2)
Jo det kan du, men du måste räkna rätt.
Förstår du?
advodis skrev:Som svar på min egna tidigare fråga, kan det vara för att man behöver ha två termer, a & b, som i formeln för komplexa tal för att beräkna svaret?
Jag förstår inte riktigt din fråga. Kan du omformulera den?
JohanF skrev:advodis skrev:Som svar på min egna tidigare fråga, kan det vara för att man behöver ha två termer, a & b, som i formeln för komplexa tal för att beräkna svaret?
Jag förstår inte riktigt din fråga. Kan du omformulera den?
OK, nu förstår jag vad du syftar på. Nä, det har med Eulers formel att göra. Eulers formel säger att , och för att kunna identifiera vinkeln så måste du på något sätt först skriva om ditt komplexa tal till formen (och sedan använda arctan etc...)
Alternativt göra på det andra sättet jag beskrev, att först skriva om täljare och nämnare med Euler formel (det kan du göra eftersom både täljare och nämnare är skrivna på formen a+jb), och sedan använda potenslagar för division.
JohanF skrev:JohanF skrev:advodis skrev:Som svar på min egna tidigare fråga, kan det vara för att man behöver ha två termer, a & b, som i formeln för komplexa tal för att beräkna svaret?
Jag förstår inte riktigt din fråga. Kan du omformulera den?
OK, nu förstår jag vad du syftar på. Nä, det har med Eulers formel att göra. Eulers formel säger att , och för att kunna identifiera vinkeln så måste du på något sätt först skriva om ditt komplexa tal till formen (och sedan använda arctan etc...)
Alternativt göra på det andra sättet jag beskrev, att först skriva om täljare och nämnare med Euler formel (det kan du göra eftersom både täljare och nämnare är skrivna på formen a+jb), och sedan använda potenslagar för division.
Nu förstår jag. Tack återigen för all hjälp!