Elektrostatik uttrycka elektriskt fält med superposition
Hej, för en laddad cylinder med radie a vill jag göra följande:
Superposition
– Betrakta endast den inre ledaren (för enkelhetens skull) och anta en given ytladdningsfördelning ρs. Hur varierar ytladdningsfördelningen ρs i rummet?
– Välj ett koordinatsystem och dess origo för de beräkningar som följer.
– Skriv ner källpunkten givet det valda koordinatsystemet.
– Skriv ner fältpunkten givet det valda koordinatsystemet.
– Beräkna skillnadsvektorn .
– Beräkna dess storlek .
– Skriv ner superpositionsintegralen för det elektriska fältet baserat på resultaten ovan och förenkla om möjligt. (Observera att du inte ska försöka hitta primitivfunktionen!)
∗ Vad är riktningen för det elektriska fältet?
∗ Vilka rumskoordinater beror det elektriska fältet på?
----
Nedan har jag gjort allt detta. Jag vet att det elektriska fältet endast har radiell riktning, men hur visar jag detta matematiskt? I integralen för det elektriska fältet skalärmultiplicerar jag den infinitesimala ytvektorn med där endast komponenter överlever, men nu har jag inga riktningar kvar...

Jag har nog tänkt fel att ds' är en vektor det är nog bara ett infinitesimalt ytelement. Så jag har nu istället
, kan det förenklas mer tro?
Här har vi riktningen i täljaren, som beror av dels två olika phi och två olika z, som på något sätt måste bli endast rhat riktning. Hur detta ska ske är jag osäker på.
Om cylindern är ändlig kommer fältet inte enbart ha radiella komponenter. Men jag antar att den är oändlig då det annars ofta saknas analytisk lösning på grund av komplexa randeffekter.
Om oändlig
När du löser integralen kommer du se att enbart radiell riktning blir kvar om du utför beräkningen. Det är bara att stoppa in och köra på. Bidraget från de andra riktningarna tar ut varandra på grund av symmetri. Men, det står uttryckligen att du inte ska göra det och det är jäkla tidskrävande så undvik det.
Du kan istället motivera att fältet enbart har radiell riktning genom Gauss sats. Jag antar att du känner till hur man gör med Gauss sats. Då kan du ta hand om att eliminera både - och -beroende. Annars kan du använda symmetriargument.
Alternativa symmetriargument utan explicit användning av Gauss sats
Som enkelt symmetriargument kan du bortse från -bidraget direkt eftersom du har konstant laddningsdensitet över ytan, alltså exakt samma problem oberoende av vinkel.
Det räcker att enbart hänvisa till Gauss sats utan att utföra något arbete alls genom att hävda faktumet att du kan flytta en cylindrisk, Gaussisk yta längs med din cylinder och formulera exakt samma problem. Därmed har du inget -beroende.
Detta och liknande är förövrigt frågor som mycket enkelt kan besvaras av Chat-GPT 4o.
SaintVenant skrev:Om cylindern är ändlig kommer fältet inte enbart ha radiella komponenter. Men jag antar att den är oändlig då det annars ofta saknas analytisk lösning på grund av komplexa randeffekter.
Om oändlig
När du löser integralen kommer du se att enbart radiell riktning blir kvar om du utför beräkningen. Det är bara att stoppa in och köra på. Bidraget från de andra riktningarna tar ut varandra på grund av symmetri. Men, det står uttryckligen att du inte ska göra det och det är jäkla tidskrävande så undvik det.
Du kan istället motivera att fältet enbart har radiell riktning genom Gauss sats. Jag antar att du känner till hur man gör med Gauss sats. Då kan du ta hand om att eliminera både - och -beroende. Annars kan du använda symmetriargument.
Alternativa symmetriargument utan explicit användning av Gauss sats
Som enkelt symmetriargument kan du bortse från -bidraget direkt eftersom du har konstant laddningsdensitet över ytan, alltså exakt samma problem oberoende av vinkel.
Det räcker att enbart hänvisa till Gauss sats utan att utföra något arbete alls genom att hävda faktumet att du kan flytta en cylindrisk, Gaussisk yta längs med din cylinder och formulera exakt samma problem. Därmed har du inget -beroende.
Detta och liknande är förövrigt frågor som mycket enkelt kan besvaras av Chat-GPT 4o.
Glömde tillägga att Koaxialkabeln modelleras som två mycket långa cirkulära metallcylindrar. Cylindrarna har radierna a och b>a, och längden L≫b. Vad gäller randvillkor så har vi en spänning mellan ytorna av de två. Det stod att man endast skulle fokusera på den inre till och börja med därav min post.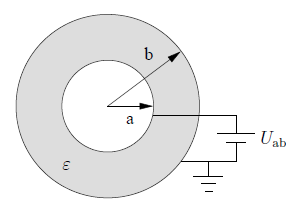
Hur kan jag förenkla superpos-integralen fullständigt?
Som det nämndes tidigare kommer inte ge något bidrag men vi kan väl inte bara ta bort det från täljaren eftersom nämnaren också beror av .
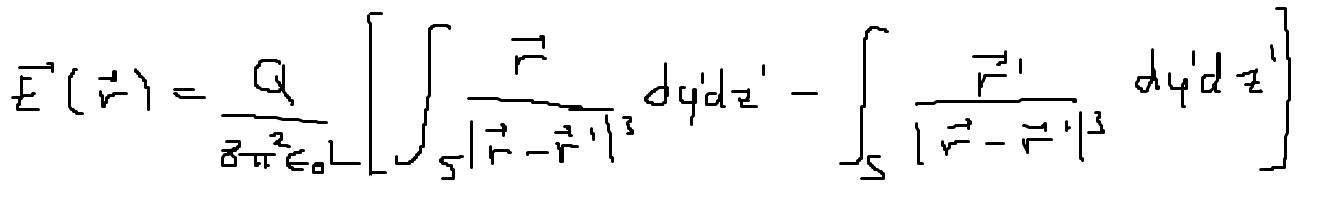
Låt mig utveckla vad jag menar. Hade den högra termen inte haft någon nämnare så hade integralen vart lika med noll här, men faktum är att vi har en nämnare som också beror på ...
Jag skulle inte separera termerna då du redan räknat fram vektordifferensen. Tänk sedan på att enbart ställa upp den radiella komponenten. Sedan vet jag inte riktigt vad du menar med "förenkla" då du vid tillräcklig "förenkling" får fram den primitiva funktionen, vilket inte verkar vara uppgiften.
Jag vet inte heller vad du menar med att inte ger något bidrag. Vad menar du? Den är ju högst relevant.
För att spara tid skulle jag fråga Chat-GPT då denne kan ge dig svar direkt:

SaintVenant skrev:Tänk sedan på att enbart ställa upp den radiella komponenten.
Det måste väl finnas en z komponent då cylindern ej är oändligt lång (den har längd L).
Bara för att säkerställa, vid superposition tar komponenter ut varandra men inte . Det måste väl finnas en z komponent så vidare vi inte tittar precis i mitten av cylinder (vid L/2).
Så riktningen för de elektriska fältet är ?
För att besvara frågan vilka rumskoordinater fältet beror på så måste det väl då vara längden på r till fältpunkten, z-koordinaten där fältpunkten är.
Cien skrev:SaintVenant skrev:Tänk sedan på att enbart ställa upp den radiella komponenten.
Det måste väl finnas en z komponent då cylindern ej är oändligt lång (den har längd L).
Nja, det vet jag inte. Uttrycket "mycket lång" betyder vanligast att och detta innebär att z-komponenten inte ger något bidrag i förhållande till det radiella, med samma resonemang som för en oändlig ledare. Alltså, att för varje skiva tar bidragen ut varandra och alla randeffekter kan bortses ifrån. Men det beror mycket på var man mäter, alltså om till exempel , om osv. vilket du också nämner.
Bara för att säkerställa, vid superposition tar komponenter ut varandra men inte . Det måste väl finnas en z komponent så vidare vi inte tittar precis i mitten av cylinder (vid L/2).
Japp. Antar att faktumet att du inte behöver lösa integralen är en hint till att du ska ta hänsyn till randeffekter, alltså inte bortse från bidraget från z-led.
Så riktningen för de elektriska fältet är ?
Naej, har inte just dessa riktningar då det som sagt blir lite knepigt speciellt vid ändarna. Men du kanske menar att fältet kan ha en komponent i dessa riktningar, i så fall ja.
För att besvara frågan vilka rumskoordinater fältet beror på så måste det väl då vara längden på r till fältpunkten, z-koordinaten där fältpunkten är.
Japp.



