Elektriskt flux
Lite problem med uppgiften nedan. Var ett tag sen man sysslade med flervariabelanalys. Jag får en jobbig integral på slutet och jag misstänker att jag har trasslat in mig i något som jag aldrig borde. Kan inte se de uppenbara. Tacksam om någon kunde leda bollen i mål.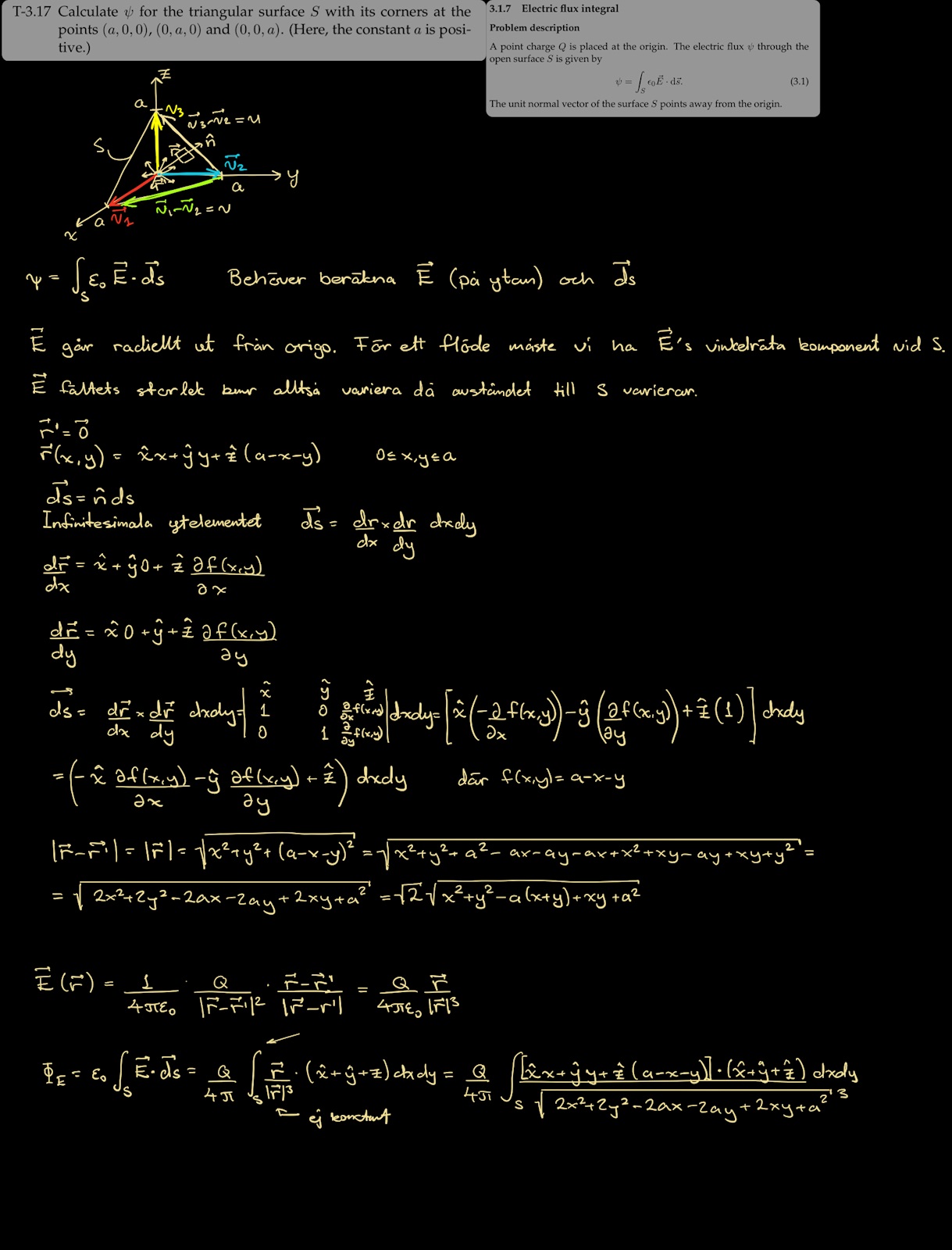
Läs kapitel 4-5 här.
Källan i origo ger ett symmetriskt flöde i alla riktningar. Som en lampa.
Flödet genom triangeln ska vara lika stort som flödet genom den del av en sfär som strålarna från origo går genom. Kan du komma på hur stor andel av sfären det är?
D4NIEL skrev:Källan i origo ger ett symmetriskt flöde i alla riktningar. Som en lampa.
Flödet genom triangeln ska vara lika stort som flödet genom den del av en sfär som strålarna från origo går genom. Kan du komma på hur stor andel av sfären det är?
Jag gissar på 1/8? då vi befinner oss i första oktanten i de 3dim rummet
Ja, och det är ju enklare än att genomföra de krångliga räkningarna tänker jag. Men om du vill kan du även genomföra räkningarna och få samma resultat. Tror dock inte det är det uppgiftsmakaren hade i åtanke :)
Möjligtvis kan du räkna ut hur stort delflödet blir genom en sfär med radien mellan vinklarna och . Då får du såklart ett resultat oberoende av sfärens radie .
D4NIEL skrev:Ja, och det är ju enklare än att genomföra de krångliga räkningarna tänker jag. Men om du vill kan du även genomföra räkningarna och få samma resultat. Tror dock inte det är det uppgiftsmakaren hade i åtanke :)
Möjligtvis kan du räkna ut hur stort delflödet blir genom en sfär med radien mellan vinklarna och . Då får du såklart ett resultat oberoende av sfärens radie .
Nu när du säger det kan jag "se" hur det "flödar" lika mycket ur den triangulära ytan som ur en 1/8 sfärisk yta. Intressant. Sen är ju också HL i Gauss-sats oberoende av ytan (Q/)
Du kan även tänka dig att du lägger till liknande triangulära ytor i alla oktanter. Du får då en sluten yta som du kan tillämpa Gauss lag på. Flödet genom den slutna ytan blir då lika med den inneslutna laddningen, dvs Q. Pga symmetri blir flödet genom ytan i första oktanten 1/8 av totala flödet. Så Q/8 borde bli svaret.
PATENTERAMERA skrev:Du kan även tänka dig att du lägger till liknande triangulära ytor i alla oktanter. Du får då en sluten yta som du kan tillämpa Gauss lag på. Flödet genom den slutna ytan blir då lika med den inneslutna laddningen, dvs Q. Pga symmetri blir flödet genom ytan i första oktanten 1/8 av totala flödet. Så Q/8 borde bli svaret.
Smart. Problemet med den triangulära ytan är väl att det elektriska fältet inte är vinkelrätt mot ytan överallt? Om du ser på min beräkning blir det en besvärlig integral
Ja, det blir en besvärlig integral, så det är säkert tänkt att man skall lösa uppgiften på de sätt som D4NIEL eller jag har föreslagit.


