Elektriskt fält och potential på sfär

Laddningen på ett sfäriskt föremål kan uttryckas som $\rho ={\rho }_0\left[1-\frac{R^2}{b^2}\right] \mathrm{C}/{\mathrm{m}}^3$ för 0 < R < b. Det laddade föremålet är omgivet av ett ledande skal med inre radie R_i (> b) och yttre radie R₀. Bestäm det elektriska fältet, E, överallt och bestäm potentialen, U, på yttre sidan av skalet.

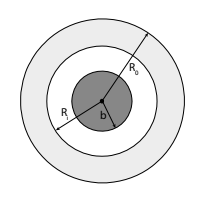
Lösningsförslaget använder Gauss lag $∯\stackrel{\rightharpoonup }{E}·d\stackrel{\rightharpoonup }{S}=\frac{Q}{\epsilon }$ och delar upp föremålets elektriska fält beroende på radie. Enligt lösningsförslaget ska det bli:

R<b:

$Q={\int }_0^R\rho ·4·\pi ·R^{2}dR={\int }_0^R{\rho }_0\left[1-\frac{R^2}{b^2}\right]·4·\pi ·R^{2}dR=4\pi {\rho }_0{\left[\frac{R^3}{3}-\frac{R^5}{5b^2}\right]}_0^R=4\pi {\rho }_0\left[\frac{R^3}{3}-\frac{R^5}{5b^2}\right]$

b<R<R_i: 

$Q=4\pi {\rho }_0\left[\frac{b^3}{3}-\frac{b^5}{5b^2}\right]=\frac{8\pi {\rho }_0{b}^3}{15}$

R_i<R<R₀:

$Q=0$

R>R₀:

$Q=4\pi {\rho }_0\left[\frac{b^3}{3}-\frac{b^5}{5b^2}\right]=\frac{8\pi {\rho }_0{b}^3}{15}$

När jag väl hittat ett uttryck för Q har jag inga problem med att använda Gauss lag för att hitta E, men det är just uttrycket för Q som jag fastnar på. 1) Hur inser man ens att man ska ta integralen av ρ multiplicerat med ytarean för klotet för att få Q? 2) Hur vet man vilka integrationsgränser man ska använda? I fallet R<b förstår jag att det blir från 0 till R, men i de andra fallen förstår jag inte. Framförallt inte varför man kan ersätta alla R med b då b<R<R_i. 3) Varför blir E=0 då R_i<R<R₀?

När jag väl förstår ovanstående och det är dags att beräkna potentialen på skalets utsida integrerar använder de $U={\int }_{R_0}^{\infty }\stackrel{\rightharpoonup }{E}d\stackrel{\rightharpoonup }{r}$. Varifrån formeln kommer förstår jag, men hur kommer det sig att man integrerar från R₀ till oändligheten?