Elektrisk potential

Lite osäker hur jag ska beräkna potentialen, och antar att det är vid "origo", dvs i mittpunkten av den inre cylindern med radie a. Jag har beräknat det elektriska fältet i en tidigare uppgift och det beskrivs nedan (krav att r>a). Jag försöker bocka av allt i integralen $V\left( \vec{r} \right)$ , det infinitesimala vektorelementet bör vara $\vec{dl}=( \hat{-r} )dr$ . Integrationsgränsen förvirrar mig lite, vi ska gå från jord till positionsvektorn, är helt lost här.

Hade uppskattat om någon kunde säga vad jag bör göra så ska jag försöka det. Tack!

Hej!

Definitionen av den elektriska potentialen i en punkt är det arbete som krävs för att förflytta en enhetsladdning från nollnivån till punkten.

Kommer du vidare?

JohanF skrev:
Hej!

Definitionen av den elektriska potentialen i en punkt är det arbete som krävs för att förflytta en enhetsladdning från nollnivån till punkten.

Kommer du vidare?

Jag tänker att jag ska använda formeln för $V\left( \vec{r} \right)$ , problemet är om vi ska gå hela vägen från jord till origo (innanför cylindern med radie a) så är det elektriska fältet inuti 0. Hur gör jag med integralen då? jag kan beräkna fram till det att vi når ytan av cylinder med radie a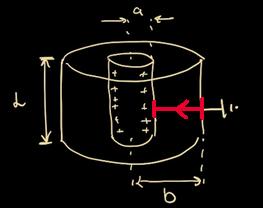

Eftersom fältet är noll inne i cylindern så är potentialen konstant där.

PATENTERAMERA skrev:
Eftersom fältet är noll inne i cylindern så är potentialen konstant där.

Juste. Då kan man nog uttrycka sambandet $\vec{E}=- \nabla \, V = 0$ . Betyder detta att jag ska integrera från jord till b-a och sen addera den konstanta delen på något sätt?

Nja, potentialen inne i cylindern blir den samma som vid r = a.

Du kan.räkna med samma integral hela vägen, men eftersom E blir noll därinne så blir ingen tillskott till integralen. Hänger du med?

JohanF skrev:
Du kan.räkna med samma integral hela vägen, men eftersom E blir noll därinne så blir ingen tillskott till integralen. Hänger du med?

Om jag gör som patenteramera säger så får jag $V (\vec{r}) = - \int_{a}^{b} \frac{Q}{2 π r L \in_{0}} \hat{r} \cdot \hat{r} d r = \frac{Q}{2 π L \in_{0}} \ln (\frac{a}{b})$

Men om jag ska använda integralen för att gå hela vägen så blir väl integrationsgränserna 0 till b? och då får vi 0 istället för a ovan, vilket ej går.

Men om jag ska använda integralen för att gå hela vägen så blir väl integrationsgränserna 0 till b? och då får vi 0 istället för a ovan, vilket ej går.

Det jag menade var att du kunde använda samma integralmetod för att beräkna potentialen då r<a (ända till r=0). Men eftersom E är noll då r<a (enligt Gauss sats) så blir integranden noll för r<a. Du måste alltså dela upp integralen i två intervall, en integral från b till a, och en integral från a till 0. Då ser man sambandet mellan potentialen vid r=a och potentialen i r=0 (se också Patenteramera's inlägg #6).

JohanF skrev:
Du måste alltså dela upp integralen i två intervall, en integral från b till a, och en integral från a till 0

Vet inte hur jag ska göra när jag sätter upp integralen från a till 0 (vi sa att potentialen var konstant här, och det elektriska fältet 0).

$V (0) - V (b) = - \int_{b}^{0} \vec{E} ∙ d \vec{r} = - \int_{b}^{a} \vec{E} ∙ d \vec{r} - \int_{a}^{0} \vec{E} ∙ d \vec{r} = - \int_{b}^{a} \vec{E} ∙ d \vec{r} - \int_{a}^{0} \vec{0} ∙ d \vec{r} = - \int_{b}^{a} \vec{E} ∙ d \vec{r} = V (a) - V (b)$

Således V(0) = V(a).

PATENTERAMERA skrev:
$V (0) - V (b) = - \int_{b}^{0} \vec{E} ∙ d \vec{r} = - \int_{b}^{a} \vec{E} ∙ d \vec{r} - \int_{a}^{0} \vec{E} ∙ d \vec{r} = - \int_{b}^{a} \vec{E} ∙ d \vec{r} - \int_{a}^{0} \vec{0} ∙ d \vec{r} = - \int_{b}^{a} \vec{E} ∙ d \vec{r} = V (a) - V (b)$

Således V(0) = V(a).

Tack ska du ha!

Svara

Visa senaste svar