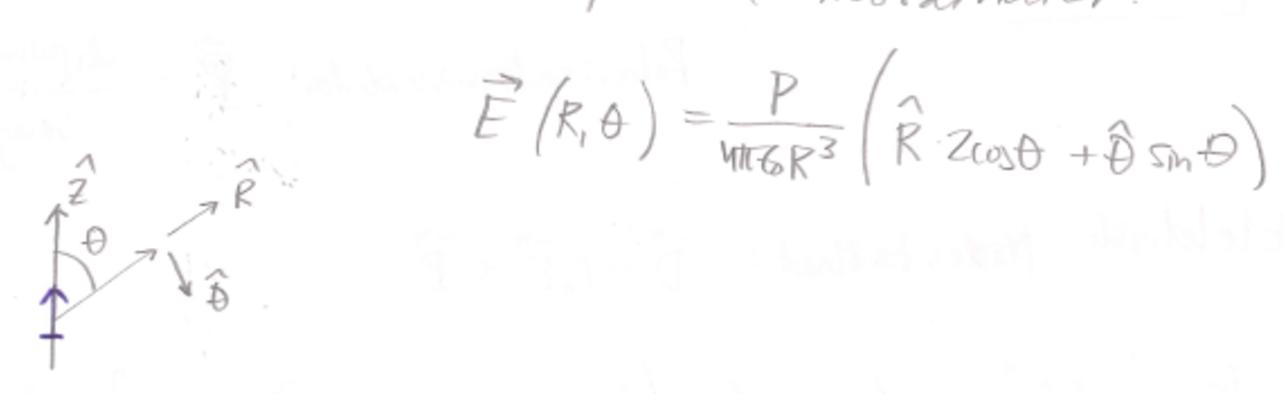Elektrisk dipol
Förstår inte facit till uppgiften nedan. Jag förstår att ˆR=ˆx när vi är nere i xy-planet. Men hur blir ˆθ=-ˆy ? borde väl peka perpendikulärt mot xy-planet, alltså i -z riktning?
Hur kan θ bero av α?
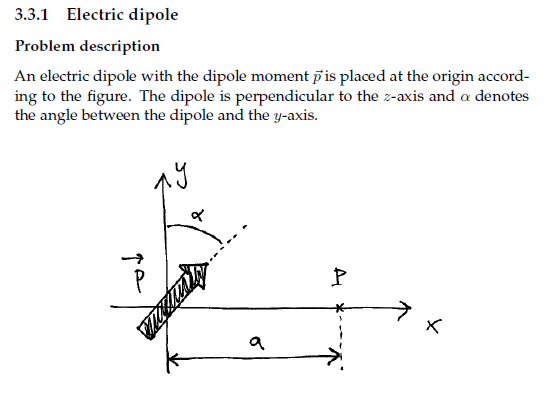
Facit: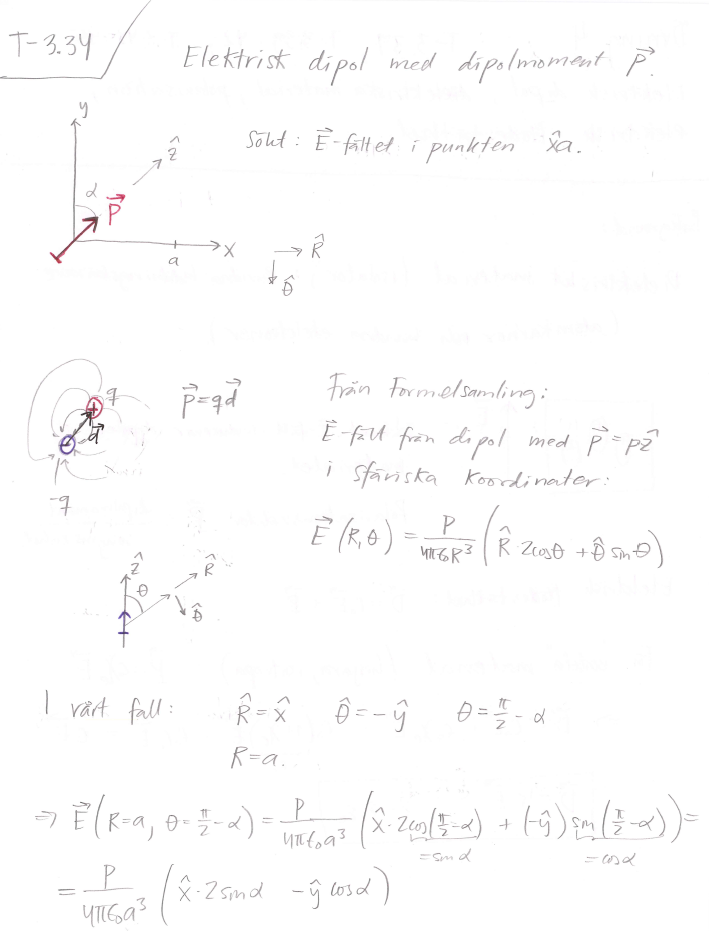
Du byter koordinatsystem från det som gäller för dipolmomentet ⇀p=p⇀z i formeln i formelbladet,
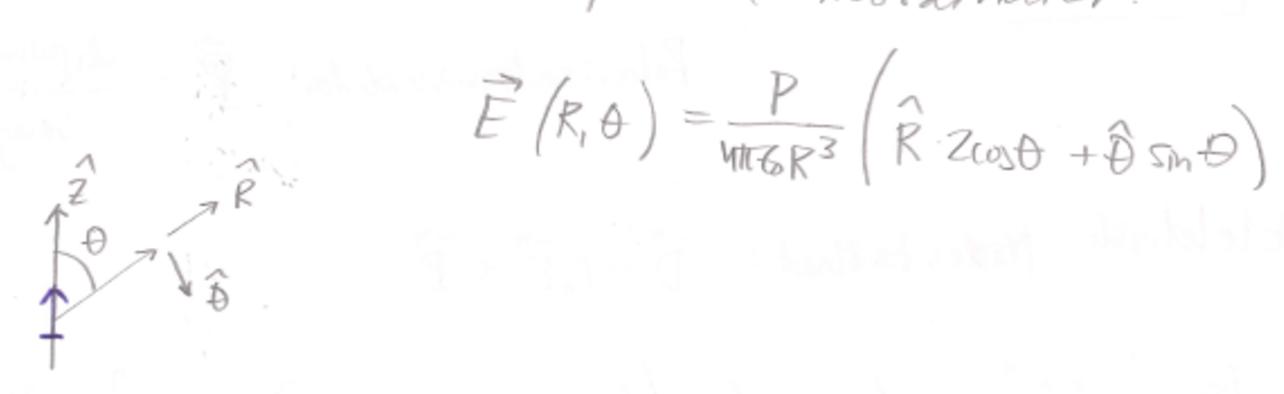
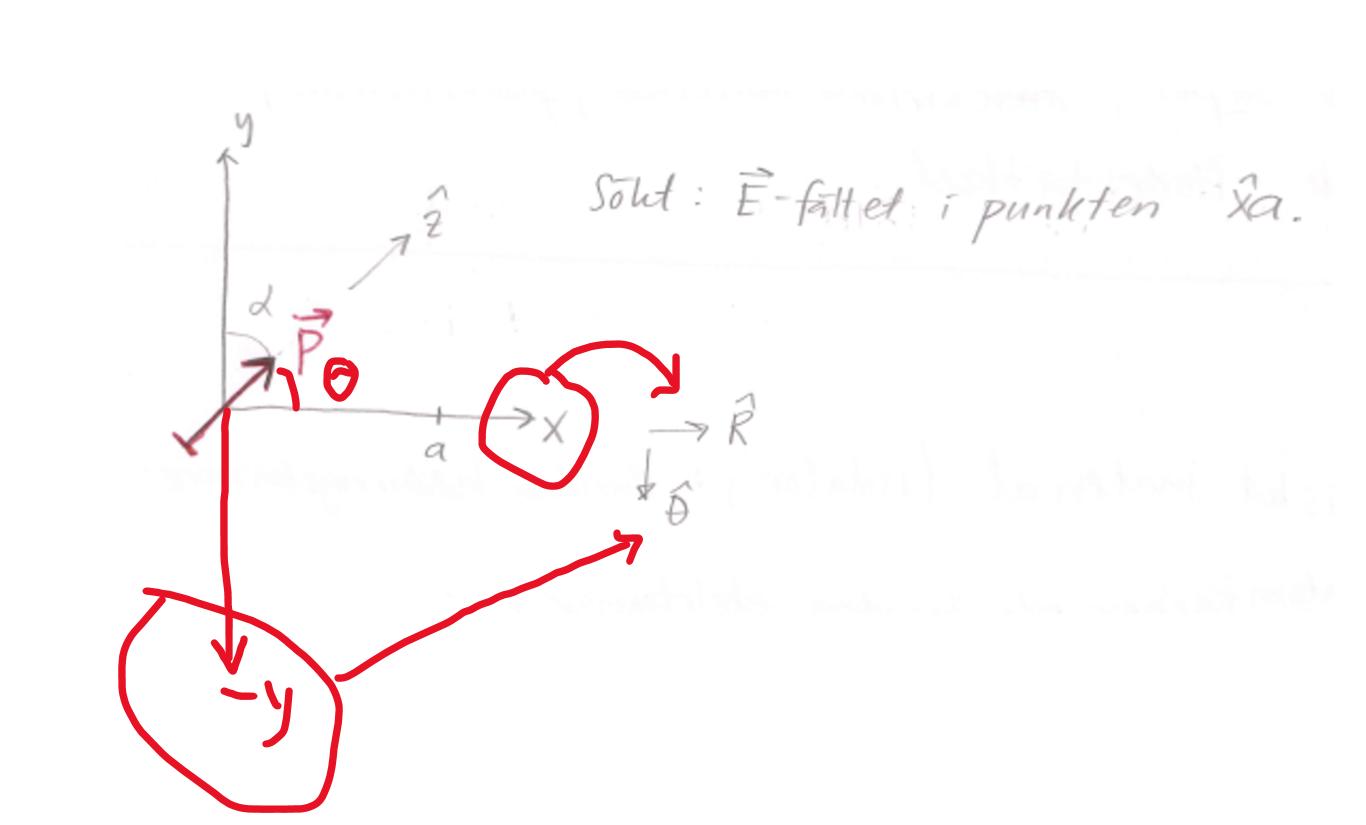
Till detta koordinatsystem:
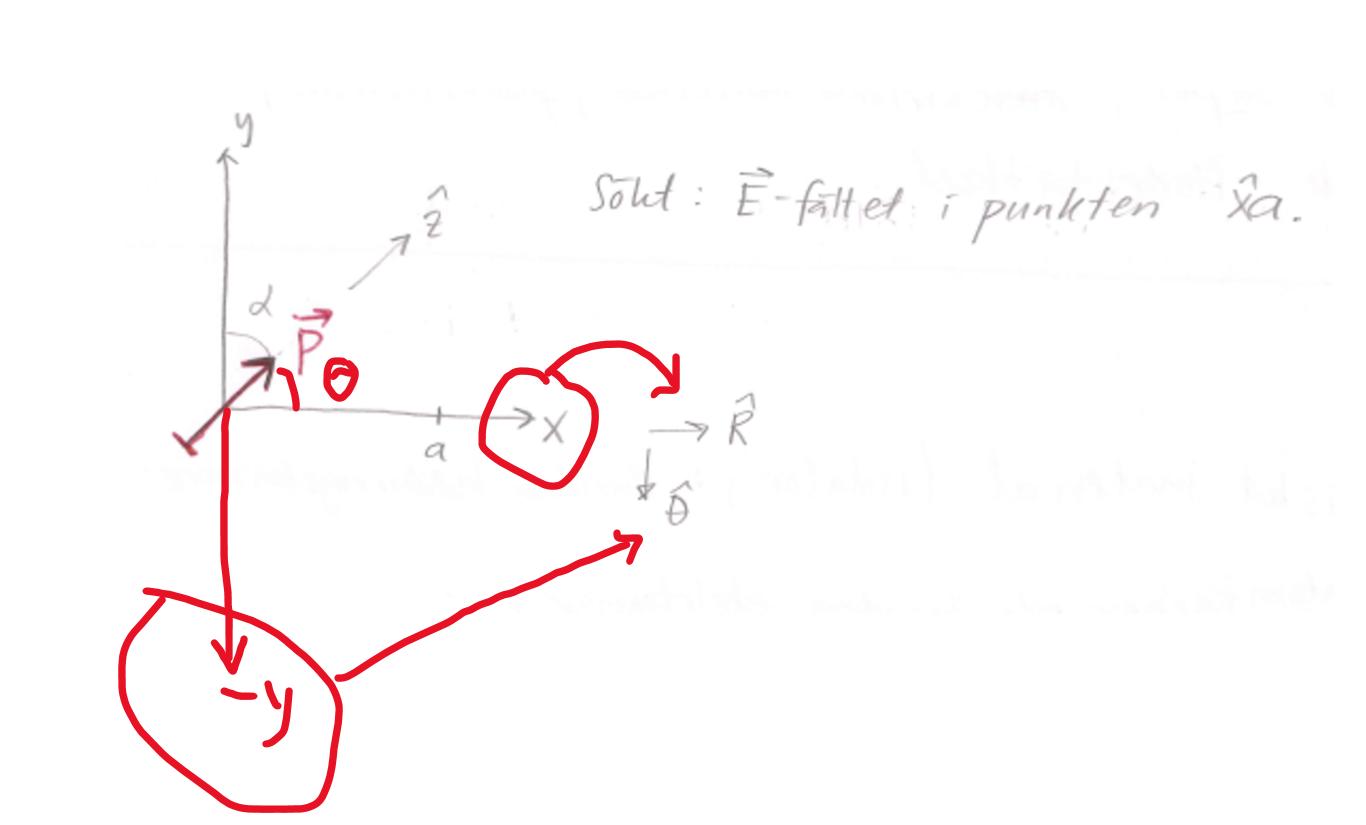
JohanF skrev:Du byter koordinatsystem från det som gäller för dipolmomentet ⇀p=p⇀z i formeln i formelbladet,
Till detta koordinatsystem:
Ok då förstår jag. Men jag får inte riktigt ihop hur →p är perpendikulär mot z axeln, och här ritar han →p parallell med ˆz. ˆz bör jag komma perpendikulärt rakt ut ur "pappret"
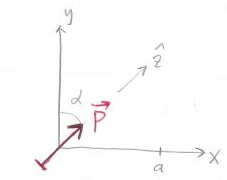
Jag fick inte heller riktigt ihop figuren som han hade ritat. Jag tror bara att han ville visa att dipolmomentet i exemplet i formelsamlingen är riktat i z-led, och att man nu måste transformera till ett annat koordinatsystem. I det nya koordinatsystemet behöver man ju inte bry sig om z-axeln.
Det är min tolkning.
JohanF skrev:Jag fick inte heller riktigt ihop figuren som han hade ritat. Jag tror bara att han ville visa att dipolmomentet i exemplet i formelsamlingen är riktat i z-led, och att man nu måste transformera till ett annat koordinatsystem. I det nya koordinatsystemet behöver man ju inte bry sig om z-axeln.
Det är min tolkning.
Okej, blev lite förvirrad där. En annan grej är att theta = pi/2 - alpha. Borde det inte vara endast theta = pi/2?
