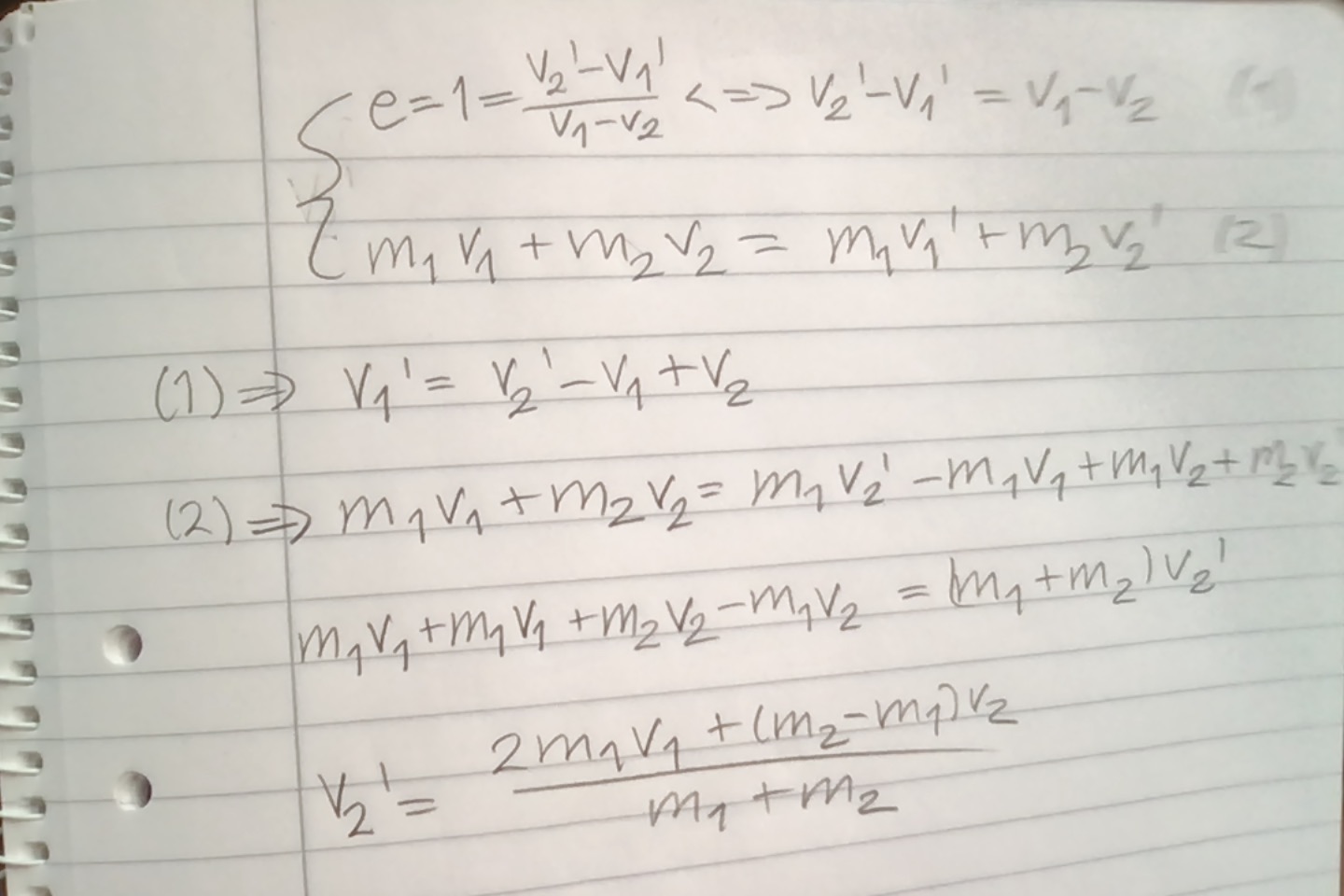Elastiska stötar
Hej!
Jag min föreläsare har sagt att vid fullständigt elastisk stöt byter partiklarna hastighet med varandra.
- Gäller det även i de fall då massorna ej är lika med varandra?
- Varför byter de hastighet istället för att båda får en medelhastighet?
Hej. Det som menas med en fullständigt elastisk stöt är att rörelseenergin före och efter kollisionen är den samma. Om massorna är olika för de två objekten som kolliderar så kommer den totala energin att förändras om man tillåter hastigheterna att byte. Man kan se det genom att låta ett objekt med 1 kg och 10 m/s kollidera med ett objekt som väger 10 kg och har hastigheten 1 m/s. Byter hastigheterna plats så fås då att den totala rörelseenergin har förändrats.
Samma anledning gäller för andra också och kan visualiseras med ett givet exempel.
Tack så mycket! Så att det sker ett "hastighetsbyte" gäller alltså bara när partiklarna som krockar har samma hastighet.
Om vi tänker oss att A har hastigheten 4 m/s och krockar med B som har 0 m/s, kommer B alltså fortsätta i samma riktning med 4 m/s medan A stannar? (A och B samma massa). Varför blir det inte så att B får hastighet framåt sqrt(8) m/s och att A studsar bakåt sqrt(8) m/s? Då bevaras ändå rörelsemängden?
För en stöt, vilken som helst, så gäller det att rörelsemängden bevaras. I fallet som du skrev är rörelsemängden innan 4*m (där massan är m) och fallet efter är då 2*sqrt(8)*m. Rörelsemängdens bevarande behöver med andra ord alltid uppfyllas vid stötar/kollisioner men vid specialfallet att det är en fullständigt elastisk stöt så behöver man ta hänsyn till rörelseenergin. Du gjorde alltså en riktig tolkning gällande rörelsemängden men man får även ta med rörelsemängden innan och efter.
Åh okej! Måste ha varit lite trött igår, nu tror jag att jag förstår. I elastiska stötar bevaras alltså både rörelsemängden och -energin, och därför byter partiklar hastighet med varandra om de har samma massa. Stämmer det?
Och om de ej har samma massa så byter de inte hastighet utan det blir på något annat sätt, som gör att både rörelseenergin och -mängden bevaras?
bump :)
Majskornet skrev:Åh okej! Måste ha varit lite trött igår, nu tror jag att jag förstår. I elastiska stötar bevaras alltså både rörelsemängden och -energin, och därför byter partiklar hastighet med varandra om de har samma massa. Stämmer det?
Och om de ej har samma massa så byter de inte hastighet utan det blir på något annat sätt, som gör att både rörelseenergin och -mängden bevaras?
Ja så blir det. Du kan ju testa själv att räkna ut det.
v1efter=2m2·v2före+(m1-m2)·v1förem1+m2.
v2efter= .
Hmm hur är det du har gjort? Får detta istället för v_1,efter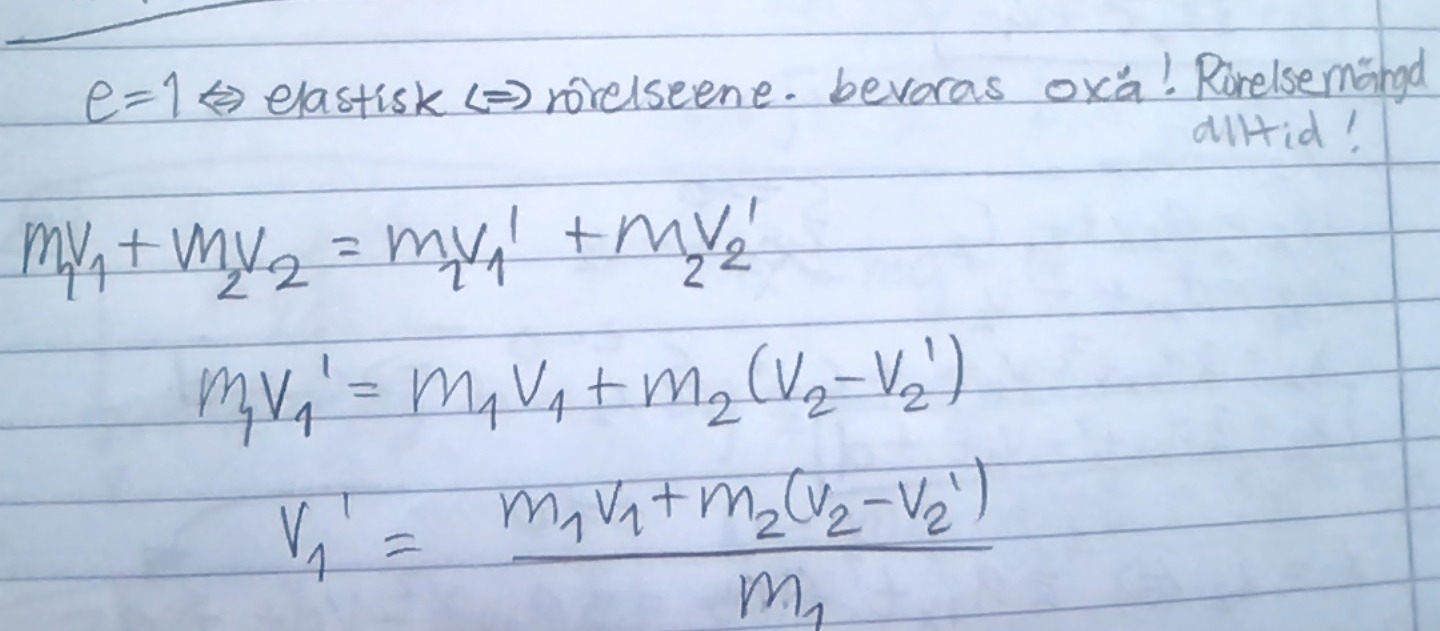
Du måste utnyttja både att rörelsemängden bevaras och att den kinetiska energin bevaras.
Att den kinetiska energin bevaras betyder att e = 1, vilket i sin tur innebär att
v1 - v2 = v’2 - v’1.
Kombinera det med rörelsemängdens bevarande.
Du får ett ekvationssystem där du kan lösa ut v’1 och v’2 i termer av v1 och v2.
Nu fick jag till det, tack för hjälpen!