Elasticitet av en exponentiation (power demand function)

Nu är jag iofs inte nationalekonom, men tanken med uppgiften är förmodligen att du ska öva på approximationen.

$\displaystyle \varepsilon=\frac{\frac{\Delta Q}{Q}}{\frac{\Delta P}{P}}=\frac{\Delta Q}{\Delta P}\frac{P}{Q}\to \frac{dQ}{dP}\frac{P}{Q}$ $\quad\quad$ När man gör förändringen oändligt  liten (dvs går i gräns).

Du kan bestämma ett värde på elasticiteten och sedan använder du värdet  för att approximera Q i en "närbelägen" punkt.

Hej, tack för ditt svar.

Självklart är meningen med uppgiften att öva på approximationen. 

Men vilket svar är "mest" rätt och vilken är en linjär approximation? Svaren är otroligt nära varandra.

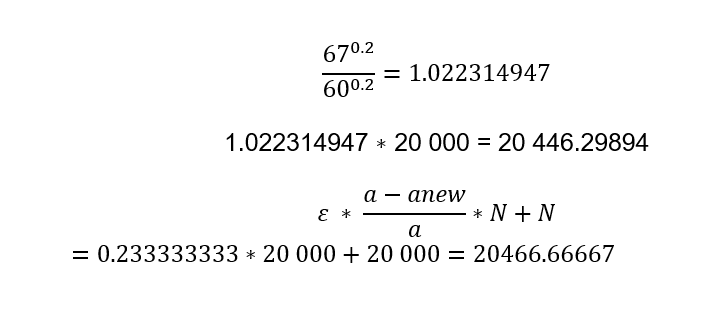
*det är ett fel där i facit. Det ska vara det andra svaret här ovan. 

Jag är inte heller nationalekonom och D4niel har säkert rätt i sitt antagande. Det har du också som jag ser det. Elasticitetsuttrycket är ju framräknat med derivatan av funktionen i a=60 och i alla andra punkter blir det ju då en (linjär) approximation om man använder den. Däremot är det ju matematiskt riktigt som du säger att du bör kunna räkna med

${\left(\frac{67}{60}\right)}^{0.2}*20000$

vilket då, som du skriver, borde ge dig ett exakt svar om funktionen för N är korrekt för  aktuella värden på a.

Skulle va intressant att höra vad en expert på ekonomi säger om det här.

En av de intressanta aspekterna här är att $\varepsilon$ blir oberoende av $a$ eftersom

$N(a)=Ca^{0.2}$

$\varepsilon=\frac{\Delta N}{\Delta a}\frac{a}{N}\to \frac{\partial N}{\partial a}\frac{a}{N}=\frac{0.2Ca^{-0.8}\cdot a}{Ca^{0.2}}=0.2$

$\Delta N\approx \varepsilon \frac{\Delta a}{a}\cdot N\approx 467$

Vilket visar sig vara en någorlunda rimlig approximation.