El- och våg: Elektrisk fält runt en laddad sfär
Tjena!
frågan lyder:
A hollow conducting spherical shell has radii of 0.80 m and 1.20 m, as shown in the figure. The sphere carries a net excess charge of -500 nC. A point charge of +300 nC is present at the center. ( = 1/4π = 8.99 × 109 N · m2/C) The radial component of the electric field at a point that is 1.50 m from the center is closest to
-2000 N/C.
+2000 N/C.
-800 N/C.
+1200 N/C.
-1600 N/C.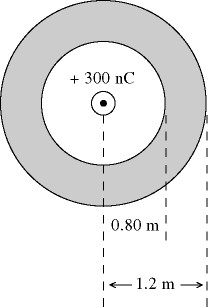
Jag förstår inte riktigt vad som frågas efter. Sfären har ju en laddning i mitten. Betyder det att sfären måste påverkas av ett motsatt fält utifrån, och är det i såna fall det jag ska räkna på?
Eftersom du inte tagit med hela frågan så är det svårt att svara på vad frågan är.
PATENTERAMERA skrev:Eftersom du inte tagit med hela frågan så är det svårt att svara på vad frågan är.
Ah, shit förlåt... Här är allt
A hollow conducting spherical shell has radii of 0.80 m and 1.20 m, as shown in the figure. The sphere carries a net excess charge of -500 nC. A point charge of +300 nC is present at the center. ( = 1/4π = 8.99 × 109 N · m2/C) The radial component of the electric field at a point that is 1.50 m from the center is closest to
-2000 N/C.
+2000 N/C.
-800 N/C.
+1200 N/C.
-1600 N/C.
Gauss lag; vad gäller för E-fältet inuti ett sfäriskt skal?
Om du har en ledare så kommer laddningarna att fördela sig på ytan av ledaren så att det inte blir något fält inuti ledaren. Det betyder att all ladding på sfären kommer att ligga på de inre och yttre begränsningsytorna. Pga av sfärisk symmetri kommer laddningen vara homogent fördelad över dessa sfäriska begränsningsytor.
Om du har en homogent laddadad sfärisk yta så är fältet innanför ytan noll och utanför är det likadant som om all ladding var koncentrerd som en punktladdning i centrum för den sfäriska ytan. Du kan visa detta med Gauss lag, med utnyttande av den sfäriska symmetrin.
Så i detta fall har du 300 nC som en punktladdning i centrum och -500 nC fördelat på sfärens begänsningsytor. Du skall utvärdera fältet i en punkt som ligger utanför sfären. Du kan göra det genom att addera ihop bidragen från punktladdningen och de två laddade sfäriska begränsningsytorna. Kommer du vidare?



