Ekvationsystem, punkten (3,a) ligger lika långt från origo som från punkten (1,5). Bestäm talet a.

Jag anar hur du har tänkt och ser vad du har skrivit, men det stämmer inte.

Om VL ska vara ett uttryck för avståndet mellan (3, a) och origo,
så borde där stå roten ur  (9 + a²)   etc.

Rita gärna figur!

stay8 skrev:

jag tänkte så här: 

 

eftersom vi vet att punkten 3.a har samma avstånd till 1.5 som den har till 0.0 så kan vi skriva så här: 

$\sqrt{{(3-0)}^2+{(a-0)}^2} = \sqrt{{(3-1)}^2+{(a-5)}^{2 }}$det är så här långt jag förstår, det skulle vara till stor hjälp om någon kan svara, ska ha prov snart. 

Jag ändrade en smula i formeln du använde; jag antar att du menade ovanstående, om inte annat för att den formeln stämmer.

Ett lämpligt nästasteg är att kvadrera såväl vänsterled som högerled. Då blir du av med de bråkiga roten-ur-tecknen.

Sedan räkna ut parenteserna, och sedan föra över alla a-termer på ena sidan om =-tecknet.

Bedinsis skrev:

stay8 skrev:

jag tänkte så här: 

 

eftersom vi vet att punkten 3.a har samma avstånd till 1.5 som den har till 0.0 så kan vi skriva så här: 

$\sqrt{{(3-0)}^2+{(a-0)}^2} = \sqrt{{(3-1)}^2+{(a-5)}^{2 }}$det är så här långt jag förstår, det skulle vara till stor hjälp om någon kan svara, ska ha prov snart. 

Jag ändrade en smula i formeln du använde; jag antar att du menade ovanstående, om inte annat för att den formeln stämmer.

Ett lämpligt nästasteg är att kvadrera såväl vänsterled som högerled. Då blir du av med de bråkiga roten-ur-tecknen.

Sedan räkna ut parenteserna, och sedan föra över alla a-termer på ena sidan om =-tecknet.

Jag tror att jag förstår vad du menar men inte riktigt. 

Jag försökte att förenkla och kom fram till $\sqrt{9+a^2} = \sqrt{4+a+25 }$men sedan för att få dessa ur roten ur så skrev jag så här $3+a = 2+..+5$,men jag förstår inte hur jag ska göra med a.

Arktos skrev:

Jag anar hur du har tänkt och ser vad du har skrivit, men det stämmer inte.

Om VL ska vara ett uttryck för avståndet mellan (3, a) och origo,
så borde där stå roten ur  (9 + a²)   etc.

Rita gärna figur!

Ja, du har helt rätt, det vara bara att jag hade skrivit grundformelen först och inte hade förenklat.

stay8 skrev:

Bedinsis skrev:

Visa föregående citat

stay8 skrev:

jag tänkte så här: 

 

eftersom vi vet att punkten 3.a har samma avstånd till 1.5 som den har till 0.0 så kan vi skriva så här: 

$\sqrt{{(3-0)}^2+{(a-0)}^2} = \sqrt{{(3-1)}^2+{(a-5)}^{2 }}$det är så här långt jag förstår, det skulle vara till stor hjälp om någon kan svara, ska ha prov snart. 

Jag ändrade en smula i formeln du använde; jag antar att du menade ovanstående, om inte annat för att den formeln stämmer.

Ett lämpligt nästasteg är att kvadrera såväl vänsterled som högerled. Då blir du av med de bråkiga roten-ur-tecknen.

Sedan räkna ut parenteserna, och sedan föra över alla a-termer på ena sidan om =-tecknet.

Jag tror att jag förstår vad du menar men inte riktigt. 

Jag försökte att förenkla och kom fram till $\sqrt{9+a^2} = \sqrt{4+a+25 }$men sedan för att få dessa ur roten ur så skrev jag så här $3+a = 2+..+5$,men jag förstår inte hur jag ska göra med a.

Det jag menar är följande:

Om 

$\sqrt{{(3-0)}^2+{(a-0)}^2} = \sqrt{{(3-1)}^2+{(a-5)}^{2 }}$

så borde även

${\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) }^2={\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)}^2$

Om vi då räknar ut vänsterledet:

$$\begin{gathered} {\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) }^2=\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) *\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) = \\ {\sqrt{{(3-0)}^2+{(a-0)}^2}}^2={(3-0)}^2+{(a-0)}^2 \end{gathered}$$

och högerledet

$$\begin{gathered} {\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)}^2=\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)*\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)= \\ {\sqrt{{(3-1)}^2+{(a-5)}^{2 }}}^2={(3-1)}^2+{(a-5)}^{2 } \end{gathered}$$

Detta eftersom att roten ur [ett tal] gånger sig själv är samma sak som att ta bort roten-ur-tecknet, så endast [ett tal] återstår.

Därmed så har vi att

${(3-0)}^2+{(a-0)}^2={(3-1)}^2+{(a-5)}^{2 }$

Känns det här begripligt?

Bedinsis skrev:

stay8 skrev:

Visa föregående citat

Bedinsis skrev:

stay8 skrev:

jag tänkte så här: 

 

eftersom vi vet att punkten 3.a har samma avstånd till 1.5 som den har till 0.0 så kan vi skriva så här: 

$\sqrt{{(3-0)}^2+{(a-0)}^2} = \sqrt{{(3-1)}^2+{(a-5)}^{2 }}$det är så här långt jag förstår, det skulle vara till stor hjälp om någon kan svara, ska ha prov snart. 

Jag ändrade en smula i formeln du använde; jag antar att du menade ovanstående, om inte annat för att den formeln stämmer.

Ett lämpligt nästasteg är att kvadrera såväl vänsterled som högerled. Då blir du av med de bråkiga roten-ur-tecknen.

Sedan räkna ut parenteserna, och sedan föra över alla a-termer på ena sidan om =-tecknet.

Jag tror att jag förstår vad du menar men inte riktigt. 

Jag försökte att förenkla och kom fram till $\sqrt{9+a^2} = \sqrt{4+a+25 }$men sedan för att få dessa ur roten ur så skrev jag så här $3+a = 2+..+5$,men jag förstår inte hur jag ska göra med a.

Det jag menar är följande:

Om 

$\sqrt{{(3-0)}^2+{(a-0)}^2} = \sqrt{{(3-1)}^2+{(a-5)}^{2 }}$

så borde även

${\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) }^2={\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)}^2$

Om vi då räknar ut vänsterledet:

$$\begin{gathered} {\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) }^2=\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) *\left(\sqrt{{(3-0)}^2+{(a-0)}^2}\right) = \\ {\sqrt{{(3-0)}^2+{(a-0)}^2}}^2={(3-0)}^2+{(a-0)}^2 \end{gathered}$$

och högerledet

$$\begin{gathered} {\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)}^2=\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)*\left( \sqrt{{(3-1)}^2+{(a-5)}^{2 }}\right)= \\ {\sqrt{{(3-1)}^2+{(a-5)}^{2 }}}^2={(3-1)}^2+{(a-5)}^{2 } \end{gathered}$$

Detta eftersom att roten ur [ett tal] gånger sig själv är samma sak som att ta bort roten-ur-tecknet, så endast [ett tal] återstår.

Därmed så har vi att

${(3-0)}^2+{(a-0)}^2={(3-1)}^2+{(a-5)}^{2 }$

Känns det här begripligt?

Ja, men när man har räknat ut parantesen och ska föra över a2 så kommer man inte att ha några a kvar, det kommer att bara finnas siffror. $$\begin{gathered} 9+a^2 =9+1+25+a^2 \\ om jag flyttar över a^2 så kommer det ena att ta ut den andra och då finns det bara siffror kvar väl. \end{gathered}$$

Eller har jag inte förstått rätt?

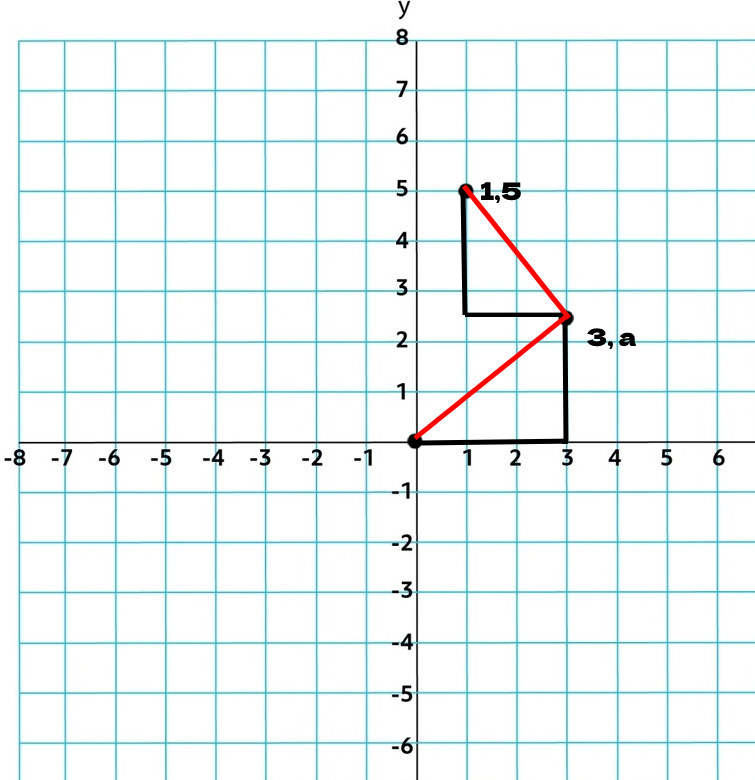
Om det Bedinsis sa inte kändes begripligt tänk såhär: 

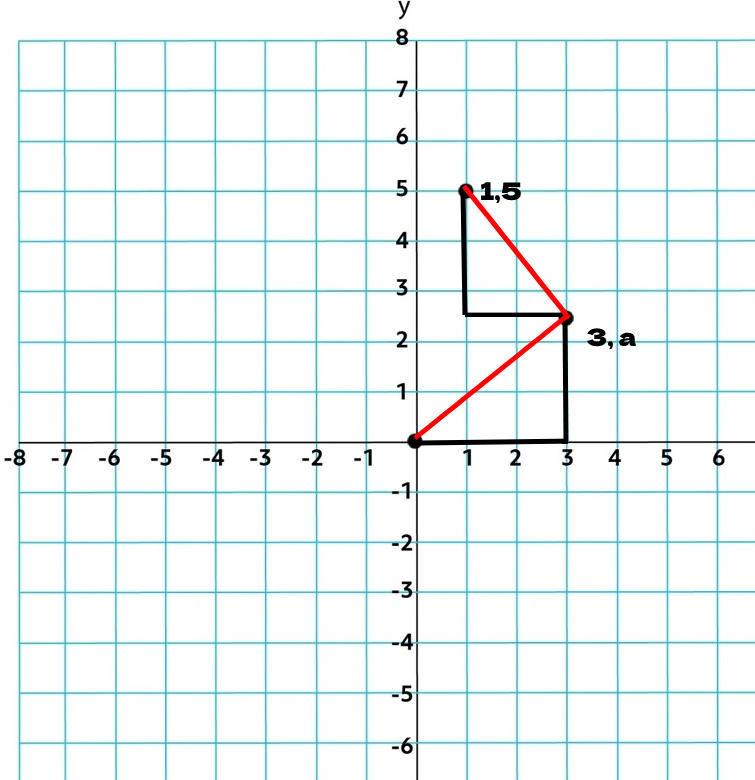
(Obs, jag valde y värdet på a slumpmässigt)

Det vi vet är att de båda röda linjerna är lika stora, och för att få ut den röda linjens längd kan man lätt göra pythagoras sats:

Nedre triangel: 

Då ser du att basen är 3 och höjden är a, då blir c^2 (dvs den röda linjen) = $\sqrt{9+a^2}$

Övre triangel: 

Här ser du att basen är 3-1 = 2 och höjden är 5-a, då blir c^2 = $\sqrt{2^2+{(5-a)}^2}$=$\sqrt{4+25-10a+a^2}$=$\sqrt{29-10a+a^2}$

Du vet att de röda linjerna är lika långa så du kan sätta båda ekvationer lika med varandra:

$\sqrt{9+a^2}\hspace{0.17em}=\hspace{0.17em}\sqrt{29-10a+a^2}$

9+a^2 = 29-10a+a^2 (ta upphöjt med två på båda sidorna för att få bort rottecknet)

9 = 29-10a (ta minus a^2 på båda sidorna)

20 = 10a

a = 2

Ja, men när man har räknat ut parantesen och ska föra över a2 så kommer man inte att ha några a kvar, det kommer att bara finnas siffror. 9+a2 =9+1+25+a2om jag flyttar över a2 så kommer det ena att ta ut den andra och då finns det bara siffror kvar väl. 9+a2 =9+1+25+a2om jag flyttar över a2 så kommer det ena att ta ut den andra och då finns det bara siffror kvar väl. 

Eller har jag inte förstått rätt?

(3-1)^2 är inte lika med 9+1 och (a-5)^2 är inte lika med a^2 +25. 

(3-1)^2 = (2)^2 = 4 

(a-5)^2 = (a-5)(a-5)    Här får du tänka kvadreringsreglerna: 

a*a = a^2

a * -5 = -5a

-5 * a = -5a 

-5*-5 = 25 

då får du a^2 -10a + 25 

Det finns kvadreringsregler då man har ett uttryck att kvadrera. Det ser ut som att du inte riktigt behärskar dem.

Kolla nedanstående uträkning där jag försökt vara pedagogisk och färga ena parentesen röd så man ser var de olika termerna kommer ifrån.

$$\begin{gathered} {\left(a-5\right)}^2= \left(a-5\right)*\left(a-5\right)= \left(a-5\right)*\left(a-5\right)=a*\left(a-5\right)-5*\left(a-5\right)=a*a-a*5-5*a-5*(-5)= \\ a*a-a*5-5*a-5*(-5)=a^2+2*5*a+{\left(-5\right)}^2\bcancel{=}{a}^2+{\left(-5\right)}^2 \end{gathered}$$

Aloosher skrev:

Ja, men när man har räknat ut parantesen och ska föra över a2 så kommer man inte att ha några a kvar, det kommer att bara finnas siffror. 9+a2 =9+1+25+a2om jag flyttar över a2 så kommer det ena att ta ut den andra och då finns det bara siffror kvar väl. 9+a2 =9+1+25+a2om jag flyttar över a2 så kommer det ena att ta ut den andra och då finns det bara siffror kvar väl. 

Eller har jag inte förstått rätt?

 

(3-1)^2 är inte lika med 9+1 och (a-5)^2 är inte lika med a^2 +25. 

(3-1)^2 = (2)^2 = 4 

(a-5)^2 = (a-5)(a-5)    Här får du tänka kvadreringsreglerna: 

a*a = a^2

a * -5 = -5a

-5 * a = -5a 

-5*-5 = 25 

då får du a^2 -10a + 25 

Jaha okej, hade glömt att det var kvadereringsregeln man skulle använda! Tack så mycket!

Bedinsis skrev:

Det finns kvadreringsregler då man har ett uttryck att kvadrera. Det ser ut som att du inte riktigt behärskar dem.

Kolla nedanstående uträkning där jag försökt vara pedagogisk och färga ena parentesen röd så man ser var de olika termerna kommer ifrån.

$$\begin{gathered} {\left(a-5\right)}^2= \left(a-5\right)*\left(a-5\right)= \left(a-5\right)*\left(a-5\right)=a*\left(a-5\right)-5*\left(a-5\right)=a*a-a*5-5*a-5*(-5)= \\ a*a-a*5-5*a-5*(-5)=a^2+2*5*a+{\left(-5\right)}^2\bcancel{=}{a}^2+{\left(-5\right)}^2 \end{gathered}$$

Hade glömt att det var kvadereringsregeln man skulle använda! Tack så mycket för hjälpen! 

Aloosher skrev:

Om det Bedinsis sa inte kändes begripligt tänk såhär: 

(Obs, jag valde y värdet på a slumpmässigt)

Det vi vet är att de båda röda linjerna är lika stora, och för att få ut den röda linjens längd kan man lätt göra pythagoras sats:

Nedre triangel: 

Då ser du att basen är 3 och höjden är a, då blir c^2 (dvs den röda linjen) = $\sqrt{9+a^2}$

Övre triangel: 

Här ser du att basen är 3-1 = 2 och höjden är 5-a, då blir c^2 = $\sqrt{2^2+{(5-a)}^2}$=$\sqrt{4+25-10a+a^2}$=$\sqrt{29-10a+a^2}$

Du vet att de röda linjerna är lika långa så du kan sätta båda ekvationer lika med varandra:

$\sqrt{9+a^2}\hspace{0.17em}=\hspace{0.17em}\sqrt{29-10a+a^2}$

9+a^2 = 29-10a+a^2 (ta upphöjt med två på båda sidorna för att få bort rottecknet)

9 = 29-10a (ta minus a^2 på båda sidorna)

20 = 10a

a = 2

Tack så mycket, det var väldigt bra och tydligt förklarat! Tack