Ekvationslösning med komplexa tal
Hej!
Jag behöver hjälp med följande ekvation:
Jag har börjat med att förenkla ekvationen:
När jag sedan har försökt att gå vidare från detta på olika sätt, så fastnar jag alltid i slutstegen. Hur bör man tänka på denna uppgift?
Tack på förhand!
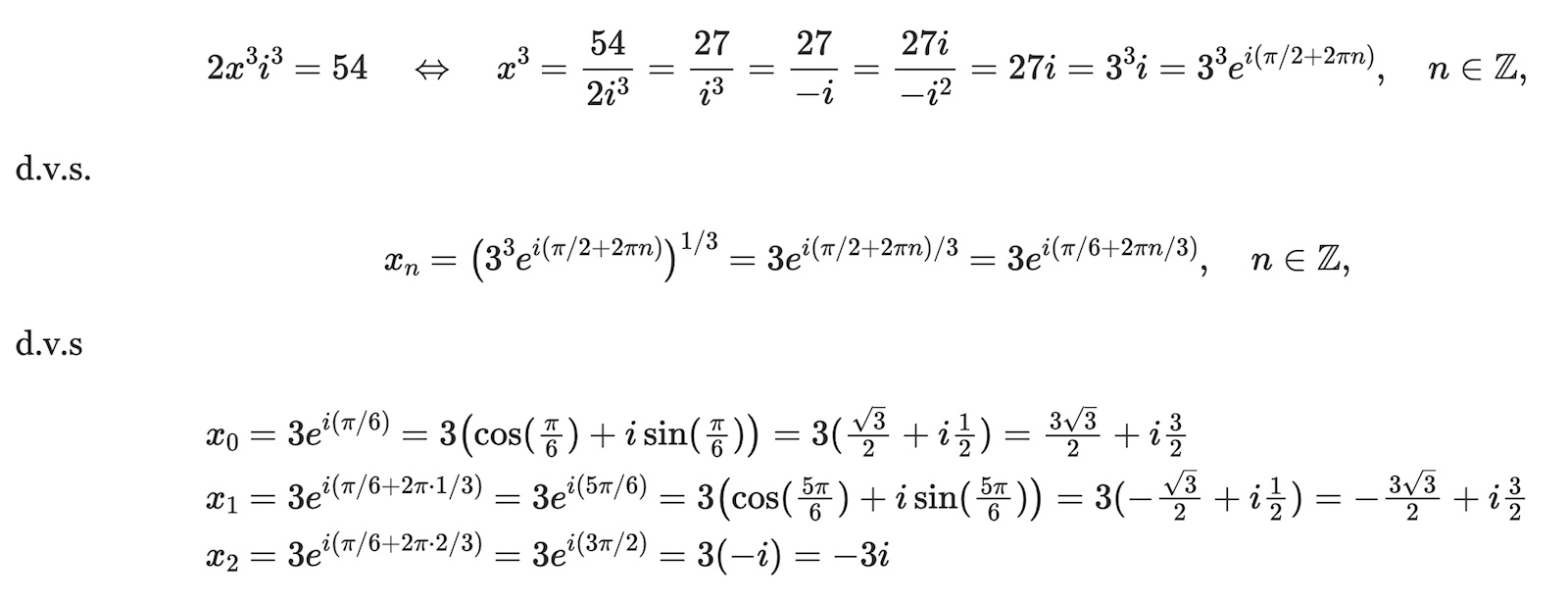
https://mathb.in/80275
Vi har inte lärt oss dessa räkneregler än. Antar att man får förenkla så långt som möjligt och sedan använda räknaren istället?
Samham skrev:Vi har inte lärt oss dessa räkneregler än. Antar att man får förenkla så långt som möjligt och sedan använda räknaren istället?
Hur långt hängde du med i Trinity2s lösning?
Har du kommit i kontakt med de Moivres formel ?
Det står inte möjligen att x ska vara ett reellt tal?
De Moivres formel introduceras 5 delkapitel efter kapitlet denna fråga finns i. Man måste ju kunna lösa den utan användning av formeln då?
Lösning till ekvationen ska ges i rektangulär form.
Det enda möjliga sättet att lösa frågan (just nu) måste väl vara att förenkla så långt som möjligt, för sedan använda räknaren då?. Tänker jag fel?
Sätt u=xi . Ekv blir då efter förenkling u3-27 =0 Den har en rot u=3. Gör polynomdivision av ekv med faktorn (u-3) så får du en andragradsekv., som du löser med pq. Tänk på att vi nu tillåter komplexa rötter! Slutligen bestämmer du rötterna till den ursprungliga ekv. genom att gå tillbaka till x.



