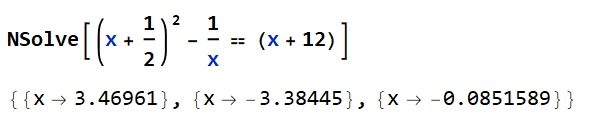Ekvationslösning

Nej, det finns inga heltal som uppfyller den ekvationen. Det blir en tredjegradare. Vi kan se det tydligt. HL är än andragradare med en faktor 1/x, HL är linjär. om du multiplicerar med x för att bli av med 1/x så har vi en tredjegradare. Om vi sedan kikar på denna tredjegradare så ser vi att det inte kan existera något heltal som uppfyller den ekvationen. Generellt sätt om du får en trejegradare så får du ofast veta en rot, eller så har den rötter du kan gissa om -2, -1, 0, 1, 2 osv.

Hur lyder hela uppgften?

Dracaena skrev:

Nej, det finns inga heltal som uppfyller den ekvationen. Det blir en tredjegradare. Vi kan se det tydligt. HL är än andragradare med en faktor 1/x, HL är linjär. om du multiplicerar med x för att bli av med 1/x så har vi en tredjegradare. Om vi sedan kikar på denna tredjegradare så ser vi att det inte kan existera något heltal som uppfyller den ekvationen. Generellt sätt om du får en trejegradare så får du ofast veta en rot, eller så har den rötter du kan gissa om -2, -1, 0, 1, 2 osv.

Hur lyder hela uppgften?

Exakt!

Jag tänker spontant att dem har gjort fel i uppgiften, men sen kommer en liknande; . Här kan vi dock se en rot vid x=1, så förmodligen går polynomdivison?

Tanke två; är det inte en fjärdegradare då det är 1/x inuti parantesen som är upphöjt i två?

Du kan sätt t=x² beroende på hur det ser ut. Jag har inte räknat. Prova!

Dracaena skrev:

Du kan sätt t=x² beroende på hur det ser ut. Jag har inte räknat. Prova!

Jag tror inte det kommer att fungera eftersom att vi har x^4,x^3,x^2 & x^1.?

Ja, roten x=1 är faktiskt en dubbelrot, men är den enda heltalsroten. Resten är komplexa.

Jag är faktiskt inte säker på vad tanken är att du skall göra. Du får ett polynom av grad 6, 5 med poldiv eftersom du nog inte ser att x=1 är en dubbelrot.

Kanske är det något vi missar? Nu har jag inte själv provat att göra poldiv med $(x-1)^2$, om du får en fin fjärdegradare där vi kan ansätta $x=t^2$ så kanske det fungerar. 

Dracaena skrev:

Ja, roten x=1 är faktiskt en dubbelrot, men är den enda heltalsroten. Resten är komplexa.

Jag är faktiskt inte säker på vad tanken är att du skall göra. Du får ett polynom av grad 6, 5 med poldiv eftersom du nog inte ser att x=1 är en dubbelrot.

Kanske är det något vi missar? Nu har jag inte själv provat att göra poldiv med $(x-1)^2$, om du får en fin fjärdegradare där vi kan ansätta $x=t^2$ så kanske det fungerar. 

Jadu, det kan jag absolut testa.Däremot slog jag in detta på flertal online equation solvers och där säger flera " No root was found algebraically". Det som känns skevt är att det finns två likadana strukturerade uppgifter, kan man göra något med faktorisering eller kan utesluta andra rötter utan att kika på hur den faktiskt ser ut?

Frågan är om du inte egentligen skall undersöka detta grafiskt? Första frågna kanske handlar om att du ska undersöka om det existerar heltal.

Om vi kikar lite på det ser vi att det inte existerar heltal.

Då kanske man blir lite fundersam var rötterna egentligen då är för den första uppgiften:

Angående 2.25:

Jag tror att tanken är att du skall undersöka denna grafiskt. Jag kan iaf inte se något smidigt sätt att lösa uppgiften. Polynomen du får är av grad >5. Som "snällast" kan vi få en fjärdegradare efter vi utför poldiv med dubbelroten x=1. Även då så måste du kunna resonera på något vis att den fjärdegradaren saknar heltalsrötter. 

Det fungerar klart om du får använda dig utav rationella rotsatsen men jag tror knappast detta tillhör matematik 4.

Finns det någon annan information högre upp vi kan relatera till uppgiften? Jag är övertygad att du skall använda desmos, grafritande miniräknar eller något liknande.

Varifrån kommer uppgiften? Är du säker på ett det är Ma4?

Smaragdalena skrev:

Varifrån kommer uppgiften? Är du säker på ett det är Ma4?

Sammanfattningsbok av gymnasiematten, så matte1-5. Detta är precis efter pol.div så det är matte 4 =)

Dracaena skrev:

Frågan är om du inte egentligen skall undersöka detta grafiskt? Första frågna kanske handlar om att du ska undersöka om det existerar heltal.

Om vi kikar lite på det ser vi att det inte existerar heltal.

Då kanske man blir lite fundersam var rötterna egentligen då är för den första uppgiften:

---

Angående 2.25:

Jag tror att tanken är att du skall undersöka denna grafiskt. Jag kan iaf inte se något smidigt sätt att lösa uppgiften. Polynomen du får är av grad >5. Som "snällast" kan vi få en fjärdegradare efter vi utför poldiv med dubbelroten x=1. Även då så måste du kunna resonera på något vis att den fjärdegradaren saknar heltalsrötter. 

Det fungerar klart om du får använda dig utav rationella rotsatsen men jag tror knappast detta tillhör matematik 4.

Finns det någon annan information högre upp vi kan relatera till uppgiften? Jag är övertygad att du skall använda desmos, grafritande miniräknar eller något liknande.

Tyvärr står det inte någon mer information om uppgiften :/ Uppgiften är ju i samband med ekvationslösningar som är så enkla som matte 2 nybörjar uppgifter. Det står inget om grafiskt någonstans.

Skriv om ekvationen så här

$\displaystyle (x+\frac{1}{x})^2-(x+\frac{1}{x})-12=0$

Låt $t=(x+\frac{1}{x})$ varvid

$t^2-t-12=0$

Lös ut $t$, lös ut $x$, tänk på att testa alla lösningar, förkasta eventuella falska rötter som uppstått vid förmodad kvadrering i sista steget.

Edit: När jag tänker närmare efter borde det inte ge några falska rötter men god vana att testa alla rötter du får ändå... :)

Snyggt D4NIEL, det ser ut som en bra idé. Funkar på båda uppgifterna.

D4NIEL skrev:

Skriv om ekvationen så här

$\displaystyle (x+\frac{1}{x})^2-(x+\frac{1}{x})-12=0$

Låt $t=(x+\frac{1}{x})$ varvid

$t^2-t-12=0$

Lös ut $t$, lös ut $x$, tänk på att testa alla lösningar, förkasta eventuella falska rötter som uppstått vid förmodad kvadrering i sista steget.

Edit: När jag tänker närmare efter borde det inte ge några falska rötter men god vana att testa alla rötter du får ändå... :)

Applåder!!!!

Dracaena skrev:

Snyggt D4NIEL, det ser ut som en bra idé. Funkar på båda uppgifterna.

Tack för att du också försökte hjälpa mig =)