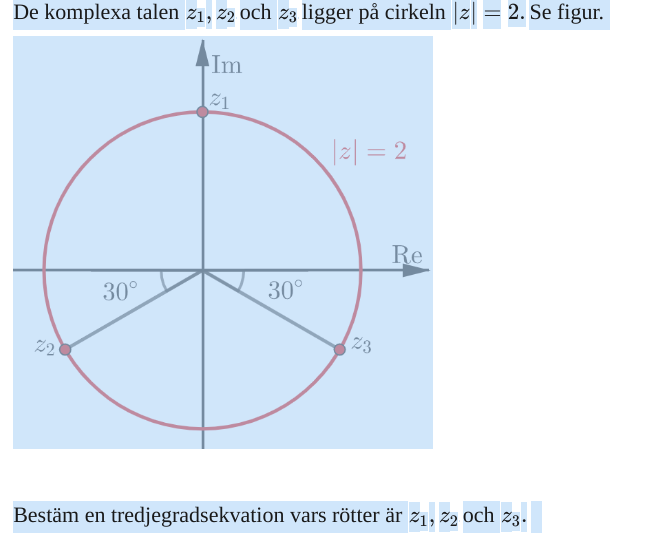
Välkommen till Pluggakuten! Börja med att uttrycka och som komplexa tal. :)
Smutstvätt skrev:Välkommen till Pluggakuten! Börja med att uttrycka och som komplexa tal. :)
Jag gjorde det och fick:
z1=2
z2,3= 2(cos(pi/6)+isin(pi/6))
Jag vet också att svaret blir -8i. Jag förstår bara inte hur de kommer fram till det. Jag försökte använda mig av "de Moivres formel" men jag vet inte hur
Ta en ny titt på detta:
z1 = 2(cos(?) + i·sin(?)) = 2i
z2 = 2(cos(-30°) + i·sin(-30°)) = 2(cos(30°) - i·sin(30°)) = …
z3 = 2(- cos(-30°) + i·sin(-30°)) = 2(- cos(30°) - i·sin(30°)) = …
Om jag nu har läst av rätt i figuren, förstås. Bäst att kolla det!
Vad är det för svar som ska bli 8i ?
I uppgiften frågas det inte efter något tal utan efter en tredjegradsekvation
med de tre givna talen som rötter.
Arktos skrev:Ta en ny titt på detta:
z1 = 2(cos(?) + i·sin(?)) = 2i
z2 = 2(cos(-30°) + i·sin(-30°)) = 2(cos(30°) - i·sin(30°)) = …
z3 = 2(- cos(-30°) + i·sin(-30°)) = 2(- cos(30°) - i·sin(30°)) = …
Om jag nu har läst av rätt i figuren, förstås. Bäst att kolla det!
Vad är det för svar som ska bli 8i ?
I uppgiften frågas det inte efter något tal utan efter en tredjegradsekvation
med de tre givna talen som rötter
-8i är tredjegradsekvationen...
-8i är väl ett tal?
En tredjegradsekvation som passar här är t ex (z-z1)(z-z2)(z-z3) = 0 .
Eller hur menar du?
Tillägg: 20 maj 2023 20:23
Menar du kanske z3 = –8i ?
Arktos skrev:-8i är väl ett tal?
En tredjegradsekvation som passar här är t ex (z-z1)(z-z2)(z-z3) = 0 .
Eller hur menar du?
Tillägg: 20 maj 2023 20:23
Menar du kanske z3 = –8i ?
Yes, menar att z^3=-8i
Bra.
Då borde du förstås ha skrivit det också.
Hur kommer man fram till den lösningen?
Se #4 och #6.
Stämmer det?
tack så mycket för hjälpen!!!