Ekvation trigonometri (Matematik/Matte 4/Trigonometri)

Om du skall finna några reella lösningar, så tror jag det står $\cos^{- 1} (\frac{1}{x + 1})$ i uppgiften.

Jag skulle börja med att rita så jag ser ungefär vad det handlar om. Kurvorna ser jag absolut inte framför mig automatiskt.

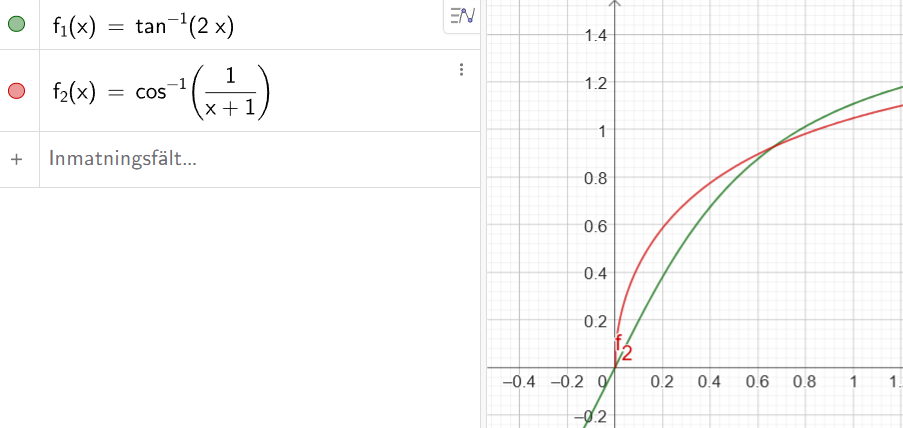
Det ser ju väldigt frestande ut att ta tan() av VL. Hittar du något i formelsamlingen om vad som då händer med HL, alltså vad tan(cos^-1(y)) är? I så fall borde det kunna vara en väg mot lösningen. Byt sedan ut y mot ditt uttryck och sedan får du något som förhoppningsvis går att förenkla.

Jag har inte provat själv, men det är hur jag skulle ge mig på problemet.

Givet att mitt intiala antagande om hur HL ser ut i uppgiften, så verkar ju en lösning för x vara nära 2/3 om man kikar på grafen.

Hej,

Har jag inte uttryckt det så? Men det är rätt i alla fall.

Ja, Jag tänkte faktiskt typ lika, men hittar ingen formel för det.

Tänker då att jag måste lista ut en sådan själv, om det är möjligt.

Dkcre skrev:
Hej,

Har jag inte uttryckt det så? Men det är rätt i alla fall.

Ja, Jag tänkte faktiskt typ lika, men hittar ingen formel för det.

Tänker då att jag måste lista ut en sådan själv, om det är möjligt.

Division före addition, så 1/x+1 är (1/x)+1.

Jag kan klura vidare, men det är lite sent för trig nu. Återkommer imorgon.

Aha okej.

Yes. Ska ligga och stirra på det lite till här, men det känns lite tungt som sagt just nu.

Tan är ju en rätvinklig triangel med ena kateten 1, borde gå att använda det på något vis

Snabb hänvisning till Wikipedia:

https://en.wikipedia.org/wiki/Inverse_trigonometric_functions

sictransit skrev:
Snabb hänvisning till Wikipedia:

https://en.wikipedia.org/wiki/Inverse_trigonometric_functions

Man kan få fram detta genom att titta på denna rätvinkliga triangel
(Jag glömde rita ut den räta vinkeln men den är rät!!)

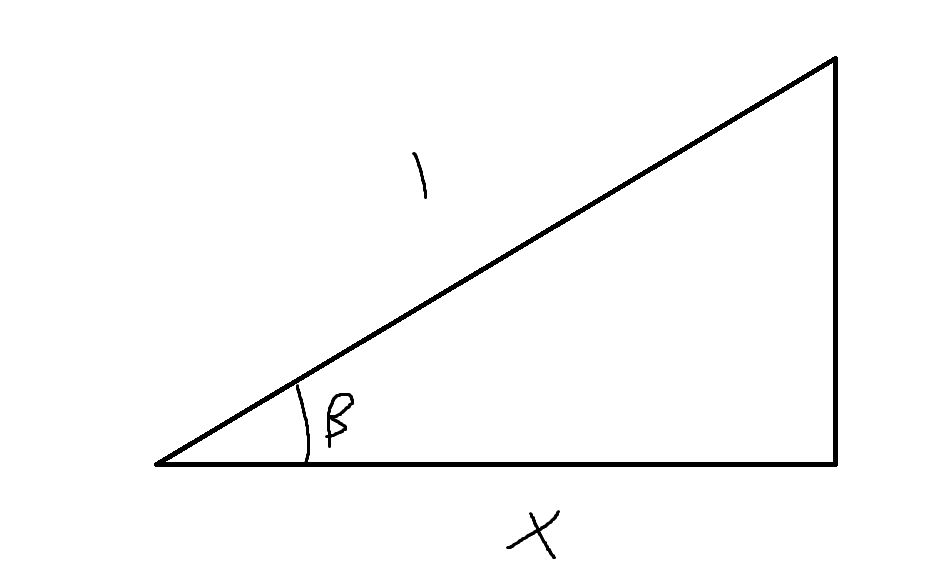
Härledning av formeln

Vinkeln som är utritad blir exakt

\displaystyle \beta = \cos^{-1} \left(\frac x1\right) = \cos^{-1} x

Med pythagoras sats kan vi få fram den sista kateten har värdet

\sqrt{1-x^2}

Tan är motstående delat med närliggande:

\tan(\cos^{-1} x) = \tan{\beta}

\displaystyle = \frac{\sqrt{1-x^2}}x

Nej, grejar det inte.

Kollade facit istället.

Man ska ta pythagoras sats på en triangel med hypotenusa (x+1) och kateter 1 och 2x. Det är enkelt, men jag hade inte kommit fram till det.