Ekvation saknar ett svar

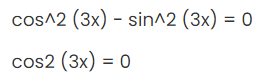
Vad är det som händer där? Vart tog $-\sin^2 3x$ vägen?

Den märkt med 1, eller fungerar inte det?

Jaha, menade du $\cos6x$? Du hade ju skrivit $(3x)$. Jo, det funkar alldeles utmärkt!

Jag blir dock lite fundersam över hur du har gjort. Jag får nämligen också de tre lösningar som facit får. Jag gör så här:

$\displaystyle \cos 6x = 0 \iff 6x = \frac{\pi}{2}+\pi n \iff x = \frac{\pi}{12}+\frac{\pi}{6}n$

Om vi begränsar oss till intervallet $\displaystyle 0 \le x \le \frac{\pi}{2}$ får vi mycket riktigt vinklarna $\pi/12, \pi/4, 5\pi/12$.

Ditt fel är att du skrev  $+360^\circ \cdot n$ istället för $+180^\circ \cdot n$.

Skrev 360*n då cos-funktionen har perioden 360. Varför blir det 180 grader nu och inte 360?

Om du börjar från $\displaystyle x=\frac{\pi}{2}$ så blir funktionen 0 varje halvt varv också. Så om du skriver $+2\pi n$ så hoppar du i princip över hälften av lösningarna. Jag svarade faktiskt ganska ingående på ungefär samma fråga i denna tråd:

https://www.pluggakuten.se/trad/berakna-den-sammanlagda-arean-av-det-skuggade-omradet/

Kanske kan det vara till hjälp? ^^

Fattar inte riktigt din metod, men handlar det om att jag glömt -15 grader?

Nej, det handlar om att när du rör dig ett helt varv i enhetscirkeln (det är det som $2\pi n$ betyder) så hoppar du över en lösning som ligger ett halvt varv bort. 

Rita en enhetscirkel och markera vinkeln $\displaystyle x = \frac{\pi}{2}$. Markera sedan nästa punkt där $\cos x = 0$. Vilken vinkel är det?

en källa till förvirring kan vara att eftersom cos(a) = cos(-a) så får vi två lösningsmängder för 

cos (6x) = 0 

6x = pi/2 +2npi

och

6x = -pi/2 + 2npi 

dessa båda lösningar kan sammanfattas som

6x = pi/2 +n*pi eftersom det skiljer exakt ett halvt varv mellan pi/2 och -pi/2 

Fattar! Tack till er båda för hjälpen :)