Dubbelspalt
Jag tycker typ facits förklaring är väldigt komplicerad. Men kan man bara tänka att interferensprickarna i mitten är centralmax och att man exempelvis sätter att vid n=4 för luft är samma som n=6 för vatten?? Eller är det bara tur att jag kunde lösa den på så sätt, för jag fick rätt våglängd
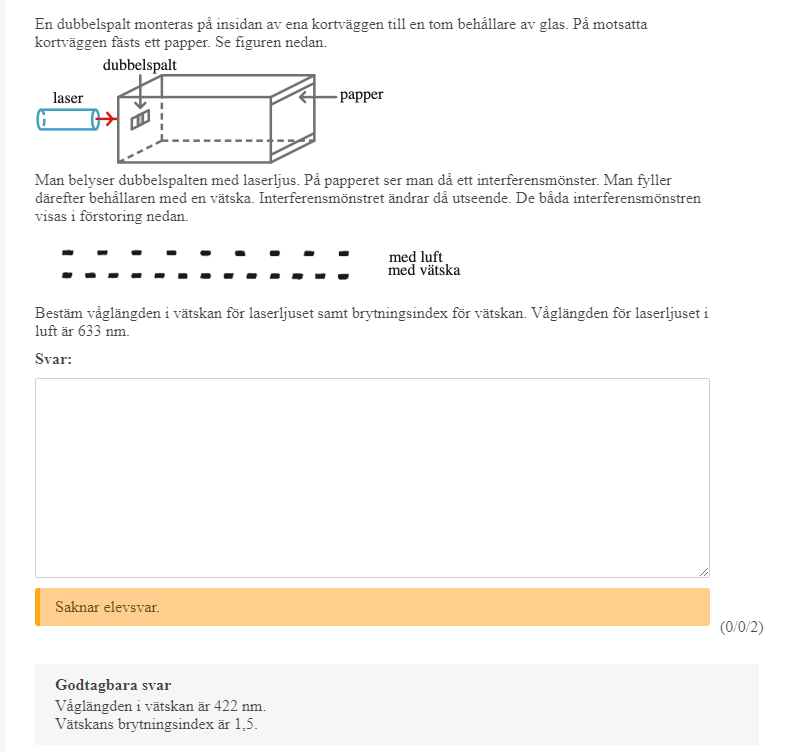

[...] kan man bara tänka att interferensprickarna i mitten är centralmax och att man exempelvis sätter att vid n=4 för luft är samma som n=6 för vatten??
Det är precis det man skriver i facit: "för varje två punkter i behållaren med luft är det tre punkter i behållaren med vätska."
(Facit struntar i vilken punkt som är centralmaximat. Det verkar gå bra här, men fungerar bara om vinklarna är små. Det verkar de ju vara, eftersom man kan se upp till sjätte ordningens maximum.)
Bubo skrev:[...] kan man bara tänka att interferensprickarna i mitten är centralmax och att man exempelvis sätter att vid n=4 för luft är samma som n=6 för vatten??
Det är precis det man skriver i facit: "för varje två punkter i behållaren med luft är det tre punkter i behållaren med vätska."
(Facit struntar i vilken punkt som är centralmaximat. Det verkar gå bra här, men fungerar bara om vinklarna är små. Det verkar de ju vara, eftersom man kan se upp till sjätte ordningens maximum.)
Så normalt sett ska man utgå från central Max?
Ja. Här ser det ut som avstånden mellan fläckarna är konstant, men det stämmer inte riktigt.
Det är ju sin(v) för avböjningsvinklarna som ökar lika mycket från en fläck till nästa.
Bubo skrev:Ja. Här ser det ut som avstånden mellan fläckarna är konstant, men det stämmer inte riktigt.
Det är ju sin(v) för avböjningsvinklarna som ökar lika mycket från en fläck till nästa.
Här är vinklarna mycket små, så .
Detta är mönstret som man ser innanför de första sidomaxima av en enkelspalt.


