Dubbelintegral
Hej!
Jag ska beräkna följande dubbelintegral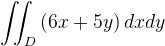 då
då  är den parallellogram som har hörn i punkterna
är den parallellogram som har hörn i punkterna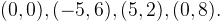
Det första och enda jag har gjort är att beräkna ekvationerna för parallellogramets sidor;
A=(0,0), B=(-5,6), C=(5,2), D=(0,8)
AB= -(6/5)x
AC= (2/5)x
BD= (2/5)x+8
CD= -(6/5)x+8
Men hur jag sedan ska gå vidare är var jag sitter fast,
Ska jag använda mig av polära koordinater? hur ska jag då göra med gränserna? vart ska jag börja är väl det som jag behöver hjälp med
Tack på förhand!
Tamino2 skrev:Hej!
Jag ska beräkna följande dubbelintegral
då
är den parallellogram som har hörn i punkterna
Det första och enda jag har gjort är att beräkna ekvationerna för parallellogramets sidor;
A=(0,0), B=(-5,6), C=(5,2), D=(0,8)
AB= -(6/5)x
AC= (2/5)x
BD= (2/5)x+8
CD= -(6/5)x+8
Men hur jag sedan ska gå vidare är var jag sitter fast,
Ska jag använda mig av polära koordinater? hur ska jag då göra med gränserna? vart ska jag börja är väl det som jag behöver hjälp med
Tack på förhand!
Börja med att rita upp området. När du har gjort detta, bör du kunna se om polära koordinater är en bra idé eller inte. Om du inte ser det själv, lägg upp din skiss här.
Smaragdalena skrev:Tamino2 skrev:Hej!
Jag ska beräkna följande dubbelintegral
då
är den parallellogram som har hörn i punkterna
Det första och enda jag har gjort är att beräkna ekvationerna för parallellogramets sidor;
A=(0,0), B=(-5,6), C=(5,2), D=(0,8)
AB= -(6/5)x
AC= (2/5)x
BD= (2/5)x+8
CD= -(6/5)x+8
Men hur jag sedan ska gå vidare är var jag sitter fast,
Ska jag använda mig av polära koordinater? hur ska jag då göra med gränserna? vart ska jag börja är väl det som jag behöver hjälp med
Tack på förhand!
Börja med att rita upp området. När du har gjort detta, bör du kunna se om polära koordinater är en bra idé eller inte. Om du inte ser det själv, lägg upp din skiss här.
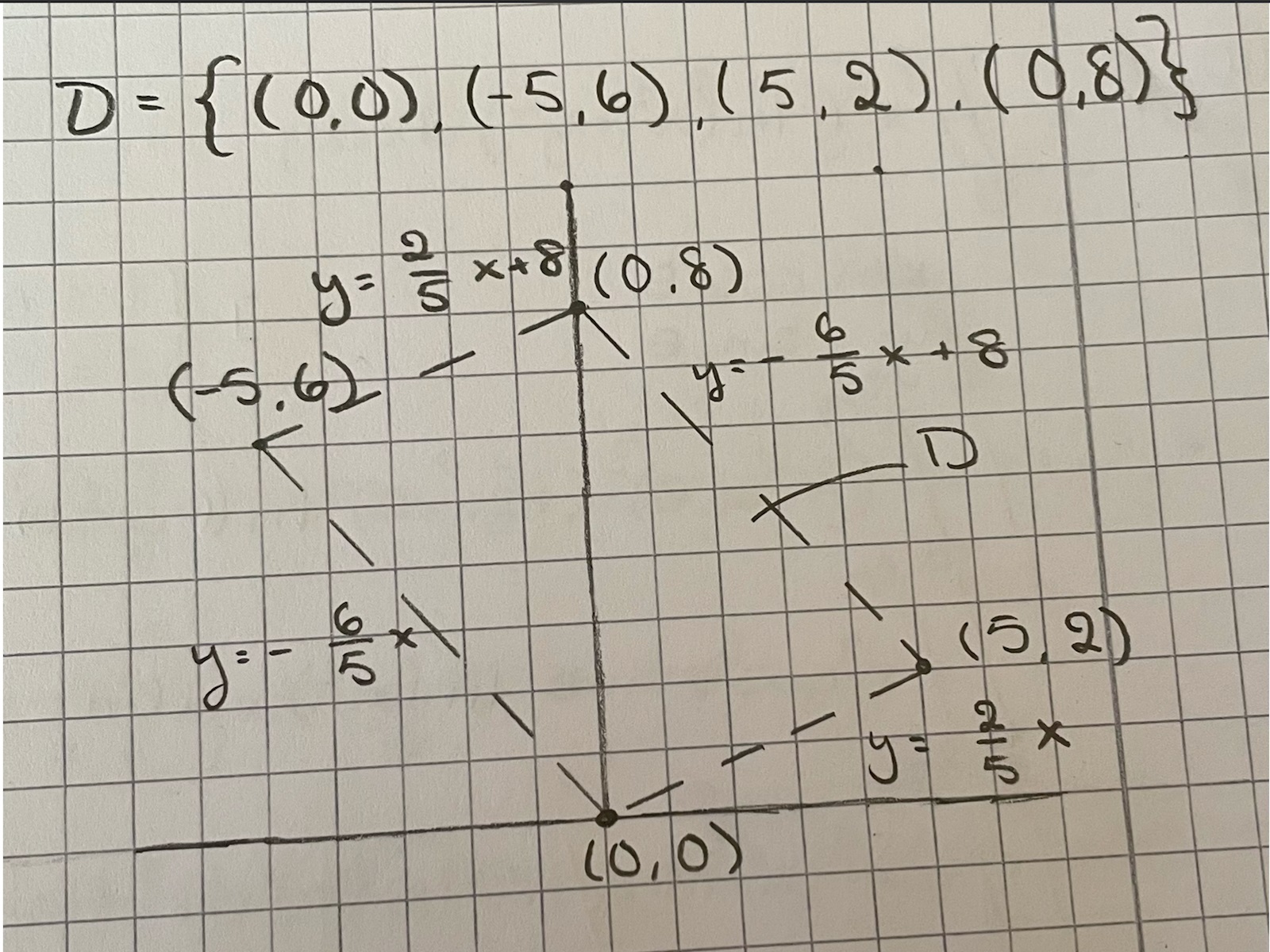
detta är den ritningen jag har gjort av parallellogramet
jag skulle tro att det går att använda polära koordinater men det som gör mig osäker är att sidorna är olika långa vilket gör mig osäker på intervallet för r i sånna fall
Se
https://www.pluggakuten.se/trad/dubbelintegral-variabelbyte-4/
Trinity2 skrev:Se
https://www.pluggakuten.se/trad/dubbelintegral-variabelbyte-4/
jag försökte följa instruktionerna men fick ej rätt svar
vad är det som jag gör fel?
Bland annat att du ska ta beloppet av Jacobianen.
Sen så borde se att din integrand blir v efter variabelbytet.
jamolettin skrev:Bland annat att du ska ta beloppet av Jacobianen.
Sen så borde se att din integrand blir v efter variabelbytet.
glömde att det inte bara var determinanten
sedan förstår jag inte riktigt vad du menar med variabelbytet och v
Du fick Jacobianen till - 1/40. Beloppet av det blir 1/40.
Din ursprungliga integral är 6x+5y.
Sen har du bytt till v=6x+5y.
Då är det väl uppenbart att din nya integral blir v.
jamolettin skrev:Du fick Jacobianen till - 1/40. Beloppet av det blir 1/40.
Din ursprungliga integral är 6x+5y.
Sen har du bytt till v=6x+5y.
Då är det väl uppenbart att din nya integral blir v.
okej då förstår jag! ska försöka igen


