Dubbelintegral

Hej!

Sitter fast med en dubbelintegral;

"Beräkna dubbelintegralen

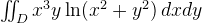där 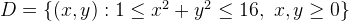Jag har omvandlat uttrycket till ett med polära koordinater vilket ger;

${\int }_0^{\mathrm{\pi }/2}{\int }_1^4{\left(r\cos \theta \right)}^3\left(r\sin \theta \right)\ln \left(r^2\right)rdrd\theta$

Sedan har jag försökt förenkla detta och samla ihop r-termerna.

${\int }_0^{\mathrm{\pi }/2}{\int }_1^4{r}^5{\cos }^3\theta \sin \theta \ln \left(r^2\right)drd\theta$

Efter detta sitter jag lite fast, kan/ska jag göra om ln(r^2) till 2ln(r)? vilket hade resulterat i

${\int }_0^{\mathrm{\pi }/2}{\int }_1^{4}2r^5\sin \theta {\cos }^3\theta \ln \left(r\right)drd\theta$

Kan jag sedan skriva om uttrycket och skilja på de olika termerna? dvs

${\int }_0^{\mathrm{\pi }/2}\sin \theta {\cos }^3\theta d\theta \times {\int }_1^{4}2r^5\ln \left(r\right)dr$

Och ska de olika integralerna multipliceras eller adderas?

Tack på förhand!