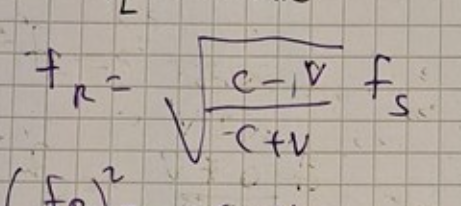
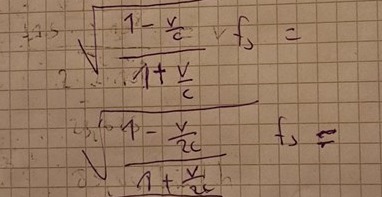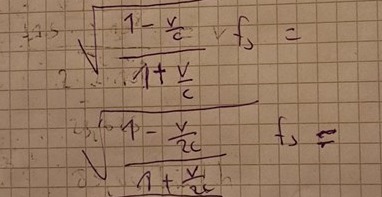Dopplereffekten för EM-vågor (Fysik/Universitet)

Använd approximationer, t ex att $\sqrt{1+\delta} \approx 1 + \delta/2$ .

Pieter Kuiper skrev:
Använd approximationer, t ex att $\sqrt{1+\delta} \approx 1 + \delta/2$ .

Det där har inte jag lärt mig tyvärr. Men vad är det som har gått snett i #1? Kan det vara så att c är ungefär lika med v=70km/h?

destiny99 skrev:
Pieter Kuiper skrev:
Använd approximationer, t ex att $\sqrt{1+\delta} \approx 1 + \delta/2$ .

Det där har inte jag lärt mig tyvärr. Men vad är det som har gått snett i #1? Kan det vara så att c är ungefär lika med v=70km/h?

Nej, c är mycket högre, det är därför du kan använda approximationen att v/c ≪ 1.

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Använd approximationer, t ex att $\sqrt{1+\delta} \approx 1 + \delta/2$ .

Det där har inte jag lärt mig tyvärr. Men vad är det som har gått snett i #1? Kan det vara så att c är ungefär lika med v=70km/h?

Nej, c är mycket högre, det är därför du kan använda approximationen att v/c ≪ 1.

ok. Vad menar du med v/c<<1? Och varför används denna approximation? Hur vet man när man ska använda den?

destiny99 skrev:
varför används denna approximation?

För att det blir mycket enklare att räkna uppgiften, man slipper andragradsekvationer.

Pieter Kuiper skrev:
destiny99 skrev:
varför används denna approximation?

För att det blir mycket enklare att räkna uppgiften, man slipper andragradsekvationer.

OK. Så hur tecknas denna approximationsformel? Jag vet att AI föreslog f=2vf₀/c som är en formel för dopplereffekten för reflekterad våg. Jag antar att det är den vi ska använda? Jag har dock aldrig sett den formeln formeln förut.

om man MacLaurinutvecklar sqrt(1+x) och tar med de två första termerna får man enl nedan,

$\sqrt{1 + x} \approx 1 + \frac{x}{2}$

Du hade kommit fram till

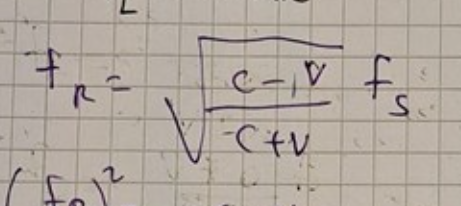
Täljaren under rottecknet kan du skriva om som

1-v/c

och nämnaren blir med samma omskrivnign

1+v/c

om du sen tillämpar Pieters förenkling

blir det

$f_{r} = \frac{1 - \frac{v}{2 c}}{1 + \frac{v}{2 c}} * f_{s}$

som går att förenkla ytterligare till 1-v/c. Kan du göra den förenklingen själv?

Då har du fått ett uttryck för den frekvens som bilen uppfattar.

Ture skrev:
om man MacLaurinutvecklar sqrt(1+x) och tar med de två första termerna får man enl nedan,

$\sqrt{1 + x} \approx 1 + \frac{x}{2}$

Du hade kommit fram till

Täljaren under rottecknet kan du skriva om som

1-v/c

och nämnaren blir med samma omskrivnign

1+v/c

om du sen tillämpar Pieters förenkling

blir det

$f_{r} = \frac{1 - \frac{v}{2 c}}{1 + \frac{v}{2 c}} * f_{s}$

som går att förenkla ytterligare till 1-v/c. Kan du göra den förenklingen själv?

Då har du fått ett uttryck för den frekvens som bilen uppfattar.

Vad menar du med ytterligare förenkling till 1-v/c? Jag kommer ingenvart med förenklingen som du fått fram.

destiny99 skrev:
Ture skrev:
$f_{r} = \frac{1 - \frac{v}{2 c}}{1 + \frac{v}{2 c}} * f_{s}$

som går att förenkla ytterligare till 1-v/c. Kan du göra den förenklingen själv?

Då har du fått ett uttryck för den frekvens som bilen uppfattar.

Vad menar du med ytterligare förenkling till 1-v/c? Jag kommer ingenvart med förenklingen som du fått fram.

Använd $\dfrac{1}{1-\delta} \approx 1+\delta$ .

Så räknar man väl ofta? Att 1/0,999 ≈ 1,001 till exempel.

Såhär får jag i uttrycket. Du verkar ha en 2a i nämnaren framför c som jag inte vet var du hämtar ifrån.

destiny99 skrev:
Ture skrev:
$f_{r} = \frac{1 - \frac{v}{2 c}}{1 + \frac{v}{2 c}} * f_{s}$

som går att förenkla ytterligare till 1-v/c. Kan du göra den förenklingen själv?

Då har du fått ett uttryck för den frekvens som bilen uppfattar.

Vad menar du med ytterligare förenkling till 1-v/c? Jag kommer ingenvart med förenklingen som du fått fram.

Jag borde skrivit utveckling och approximation, men ändå,

Om du förlänger

$f_{r} = \frac{1 - \frac{v}{2 c}}{1 + \frac{v}{2 c}} * f_{s}$ med nämnarens konjugat får du

$f_{r} = \frac{(1 - \frac{v}{2 c})^{2}}{(1 + \frac{v}{2 c}) * (1 - \frac{v}{2 c})^{}} * f_{s}$

Utveckla täljare och nämnare samt approximera v²/c² till 0

destiny99 skrev:

Såhär får jag i uttrycket. Du verkar ha en 2a i nämnaren framför c som jag inte vet var du hämtar ifrån.

Ja enligt inlägg 8, jag approximerar

$\sqrt{1 - \frac{v}{c}}$

till

1-v/(2c)

Ture skrev:
destiny99 skrev:

Såhär får jag i uttrycket. Du verkar ha en 2a i nämnaren framför c som jag inte vet var du hämtar ifrån.

Ja enligt inlägg 8, jag approximerar

$\sqrt{1 - \frac{v}{c}}$

till

1-v/(2c)

Aa ok. Hm varför approximerar man sqrt(1-v/c) till 1-v/2c?

Det blir enklare att räkna, och felet man inför är försummbart.

Ture skrev:

Om du förlänger
$f_{r} = \frac{1 - \frac{v}{2 c}}{1 + \frac{v}{2 c}} * f_{s}$ med nämnarens konjugat får du

Men det behövs inte, man kan approximer på en gång $\dfrac{f_r}{f_s} \approx 1 -\dfrac{v}{2c} - \dfrac{v}{2c} = 1 - \dfrac{v}{c}$ .

Sedan hade AI:et en till faktor 2 för reflektionen. Och det går nog att fråga AI:et också att förklara ytterligare.

om jag minns rätt från vågrörelseläran så får vi två frekvensskift,

När den utsända vågen träffar fordonet får vi en frekvensökning (om vi åker mot sändaren)

Den reflekterade strålningen (nu med en högre frekvens) sänds ut från bilen som rör sig och vi får ett frekvensskift till

Ture skrev:
om jag minns rätt från vågrörelseläran så får vi två frekvensskift,

När den utsända vågen träffar fordonet får vi en frekvensökning (om vi åker mot sändaren)

Den reflekterade strålningen (nu med en högre frekvens) sänds ut från bilen som rör sig och vi får ett frekvensskift till

Jag får såhär nu. Kvar blir bara det som är i täljaren multiplicerat med fs då. Så 2c uppkommer pga att det blir två f_r?

destiny99 skrev:
Jag får såhär nu

Nej. Den andra roten ska ju inte vara där! Den har du approximerat.

Pieter Kuiper skrev:
destiny99 skrev:
Jag får såhär nu

Nej. Den andra roten ska ju inte vara där! Den har du approximerat.

Kvar blir bara 1-v/2c*fs eftersom v^2/4c^2 går mot 0 som ture skrev i #12

Jag skriver med en vanlig beteckning $\beta = \dfrac{v}{c}$ .

Då har vi frekvensförhållandet $\dfrac{f_r}{f_s} = \sqrt{\dfrac{1-\beta}{1+\beta}} \approx \sqrt{1-2\beta} \approx 1 - \beta$ när $\beta \ll 1$ .

Här är det en reflektion, så frekvensförhållanden multipliceras och det blir $(\dfrac{f_r}{f_s})^2 \approx 1 - 2\beta.$

Och det spelar ingen roll i vilken ordning man tillämpar dessa approximationer.

Pieter Kuiper skrev:
Jag skriver med en vanlig beteckning $\beta = \dfrac{v}{c}$ .

Då har vi frekvensförhållandet $\dfrac{f_r}{f_s} = \sqrt{\dfrac{1-\beta}{1+\beta}} \approx \sqrt{1-2\beta} \approx 1 - \beta$ när $\beta \ll 1$ .

Här är det en reflektion, så frekvensförhållanden multipliceras och det blir $(\dfrac{f_r}{f_s})^2 \approx 1 - 2\beta.$

Och det spelar ingen roll i vilken ordning man gör dessa approximationer.

Okej , men du hoppade över en del steg också. Jag förstår att du kvadrerar förhållandet mellan frekvenserna så VL =(fr/fs)^2 och HL=(1-B)/(1+B). Vad händer sen med nämnaren om täljaren approximeras till (1-2B)?

Om du inte ser det kan du slå in det på en miniräknare med t ex β = 0,0001.

Pieter Kuiper skrev:
Om du inte ser det kan du slå in det på en miniräknare med t ex β = 0,0001.

Så 2v/c innebär reflektion? när jag räknar med 1-v/2c så blir svaret fel medan om man räknar med 1-2v/c så blir det rätt, så egentligen borde man ha approximerat $\sqrt{1 - \frac{v}{c}} \approx 1 - \frac{2 v}{c}$

destiny99 skrev:
Pieter Kuiper skrev:
Om du inte ser det kan du slå in det på en miniräknare med t ex β = 0,0001.

Så 2v/c innebär reflektion? när jag räknar med 1-v/2c så blir svaret fel medan om man räknar med 1-2v/c så blir det rätt, så egentligen borde man ha approximerat $\sqrt{1 - \frac{v}{c}} \approx 1 - \frac{2 v}{c}$

Kolla med miniräknare: $\sqrt{0,\!9999} \approx 0,\!99995$ .

Inte 0,9998.

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Om du inte ser det kan du slå in det på en miniräknare med t ex β = 0,0001.

Så 2v/c innebär reflektion? när jag räknar med 1-v/2c så blir svaret fel medan om man räknar med 1-2v/c så blir det rätt, så egentligen borde man ha approximerat $\sqrt{1 - \frac{v}{c}} \approx 1 - \frac{2 v}{c}$

Kolla med miniräknare: $\sqrt{0,\!9999} \approx 0,\!99995$ .

Inte 0,9998.

ok ja det stämmer, jag antar att det är bättre att approximera sqrt(1-2v/c)=1-v/c isåfall för att likheten ska stämma