Division med uttryck (Matematik/Årskurs 8)

Helt rätt. Bra!

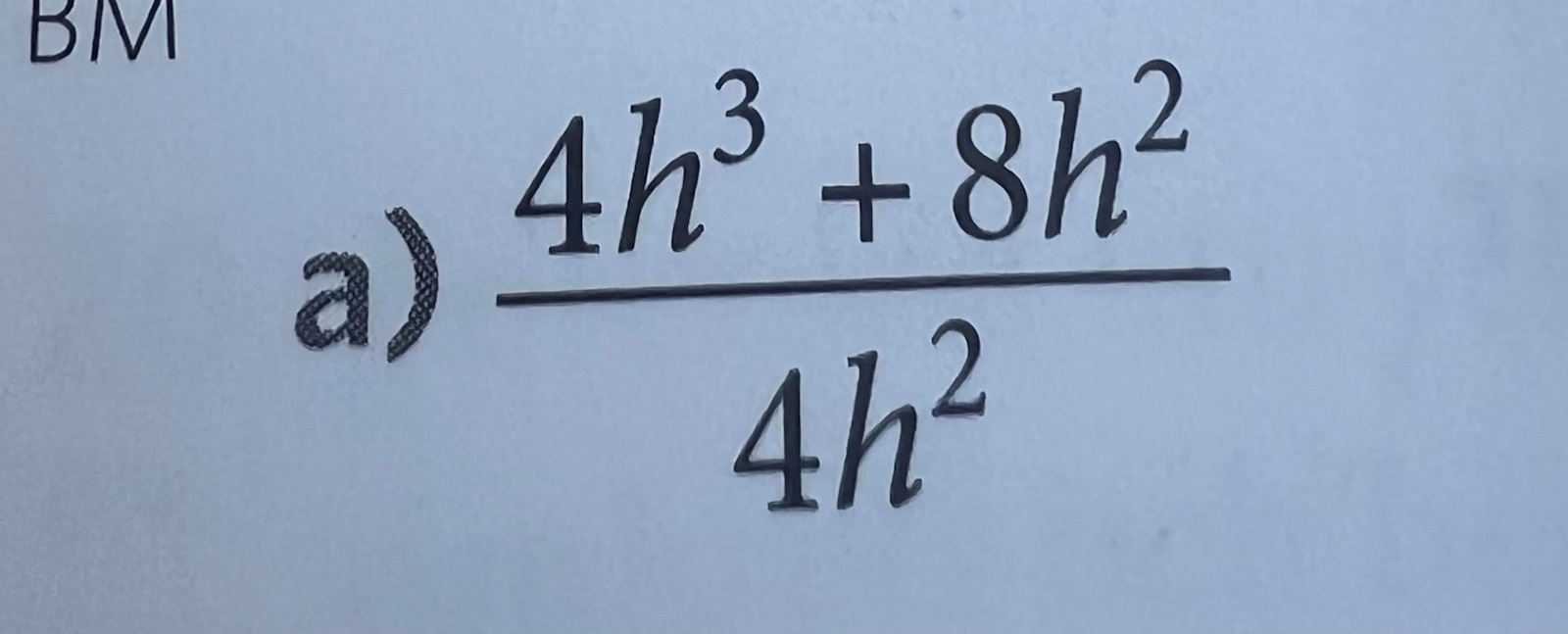
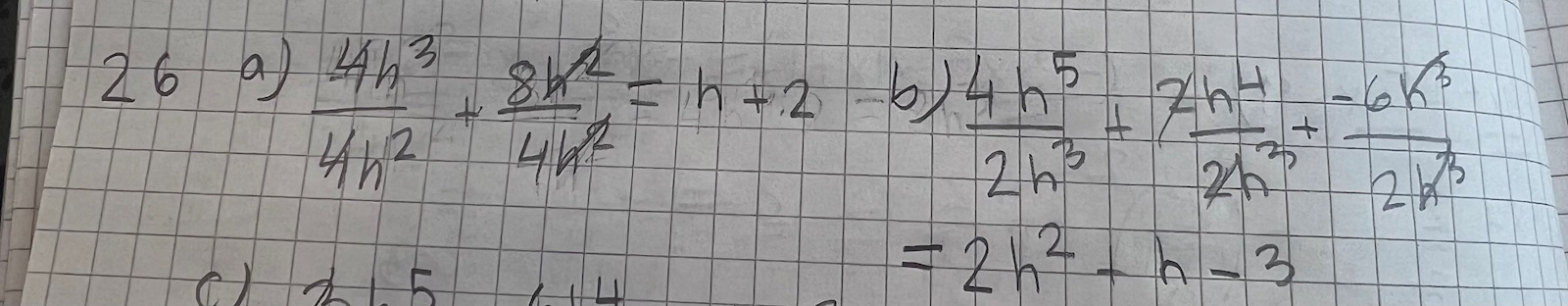Men vad är skillnaden med t.ex. denhär uppgiften. På den första täljaren så har inte variabeln samma gradtal som nämnaren, men ändå delar man på täljarna med nämnaren?

i förra uppgiften tänkte jag att det var för att den ena täljaren inte hade samma gradtal och då delade jag med 1 istället.

Finns det någon regel som man alltid ska tänka på så det blir rätt hela tiden?

Där kan man faktorisera täljaren genom att bryta ut gemensamma faktorer ur de två termerna.

Eftersom $4h^3+8h^2$ kan skrivas som $4h^2\cdot h+4h^2\cdot2$ så ser vi att $4h^2$ är en gemensam faktor i de båda termerna och vi kan då bryta ut denna faktor, vilket ger oss täljaren $4h^2(h+2)$

Bråktalet blir alltså $\frac{4h^2(h+2)}{4h^2}$ och vi kan då förkorta bråket med $4h^2$ , vilket ger resultatet $h+2$ .

Säg till om några av dessa begrepp känns obekanta, vi hjälper gärna dig att förstå dem ordentligt.

Varför bryter man ut 4h^2 när det är addition. Om man tar bort det blir väl svaret ett annat på additionen? Varför tar man bara bort den på ena sidan?

Kan någon svara snabbt för har prov om en halvtimme?😅😇

Jag är osäker på vad som är oklart, men här är en mer utförlig uträkning som kanske förklarar:

$\frac{4 * h^{3} + 8 * h^{2}}{4 * h^{2}} = \frac{4 * h * h * h + 8 * h * h}{4 * h * h} = \frac{4 * h * h * h}{4 * h * h} + \frac{2 * 4 * h * h}{4 * h * h} = \frac{4 * h * h * h}{4 * h * h} + \frac{2 * 4 * h * h}{4 * h * h} = \frac{h * h * h}{h * h} + \frac{2 * h * h}{h * h} = \frac{h * h * h}{h * h} + \frac{2 * h * h}{h * h} = \frac{h}{1} + \frac{2}{1} = h + 2$

För att besvara frågan varför man bryter ut 4*h² så är det för att det är den största gemensamma faktorn i de två termerna 4*h³ och 8*h².

Varför delar man med 1 på första uppgiften och inte på den andra?

Om man delar något med ett är värdet oförändrat så på sätt och vis kan man säga att man delar med ett på alla uppgifter. Se sista raden i min uträkning i inlägg #7. Man delar oftast med ett om man vill ha uttrycket som ett bråk.

varför delar man inte 4a^3 med 6a^2 ?

Här är det multiplikation, så det som står i täljaren är egentligen 12*a⁵. Delar man det med 6*a² får man som du kom fram till 2*a³. Att du gjorde uppdelningen att försöka stryka faktorer i första faktorn gick definitivt bra, och att du såg att det gav en snäll uträkning var bra, men man behöver inte gå den vägen.

Lycka till med provet.

Ebba123456789 skrev:
Kan någon svara snabbt för har prov om en halvtimme?😅😇

@Ebba123456789, det är inte tillåtet att bumpa sitt inlägg 24h inom sitt senaste inlägg. Volontärerna på Pluggakuten svarar i den takt de kan och vill. /moderator

Ebba123456789 skrev:
varför delar man inte 4a^3 med 6a^2 ?

Det kan du göra.

Jag antar att du är bekant med räkneregeln $b\cdot\frac{c}{d}=\frac{b\cdot c}{d}$

Denna räkneregel "baklänges" gör att du kan skriva $\frac{3a^2\cdot4a^3}{6a^2}$ som $3a^2\cdot\frac{4a^3}{6a^2}$ , vilket efter förenkling blir $3a^2\cdot\frac{2a}{3}$ .

Nu kan du "multiplicera upp" faktorn $3a^2$ i täljaren igen och du får då $\frac{3a^2\cdot2a}{3}$ , vilket efter förkortning med 3 ger $2a^3$ .

=====

Men det enklaste är nog att förkorta ursprungsbråket först med 3, sedan med 2 och slutligen med a²