Divergent dubbelintegral: beskriva området vid koordinatbyte

Hej! Jag har en fråga vart någonstans det är mitt resonemang brister i den här frågan:

Jag tänker att $x=y$ motsvaras av $\frac y x = v= 1$ , vilket stämmer. Det jag tänkte sedan var att eftersom den positiva y-axeln begränsar området, så borde det gälla att $v\geq 0$ . Detta stämmer däremot inte överrens med lösningsförslaget, som endast använder att $v\geq 1$ och får således integralen till divergent. Jag förstår att något är fel med mitt resonemang att $v\geq 0$ , jag försöker bara visualisera hur det är fel (det resonemanget ger nämligen en konvergent integral). Lösningsförslag samt uppgift nedan:

coffeshot skrev:
Hej! Jag har en fråga vart någonstans det är mitt resonemang brister i den här frågan:

Jag tänker att $x=y$ motsvaras av $\frac y x = v= 1$ , vilket stämmer. Det jag tänkte sedan var att eftersom den positiva y-axeln begränsar området, så borde det gälla att $v\geq 0$ . Detta stämmer däremot inte överrens med lösningsförslaget, som endast använder att $v\geq 1$ och får således integralen till divergent. Jag förstår att något är fel med mitt resonemang att $v\geq 0$ , jag försöker bara visualisera hur det är fel (det resonemanget ger nämligen en konvergent integral). Lösningsförslag samt uppgift nedan:

Här får du en bild över området:

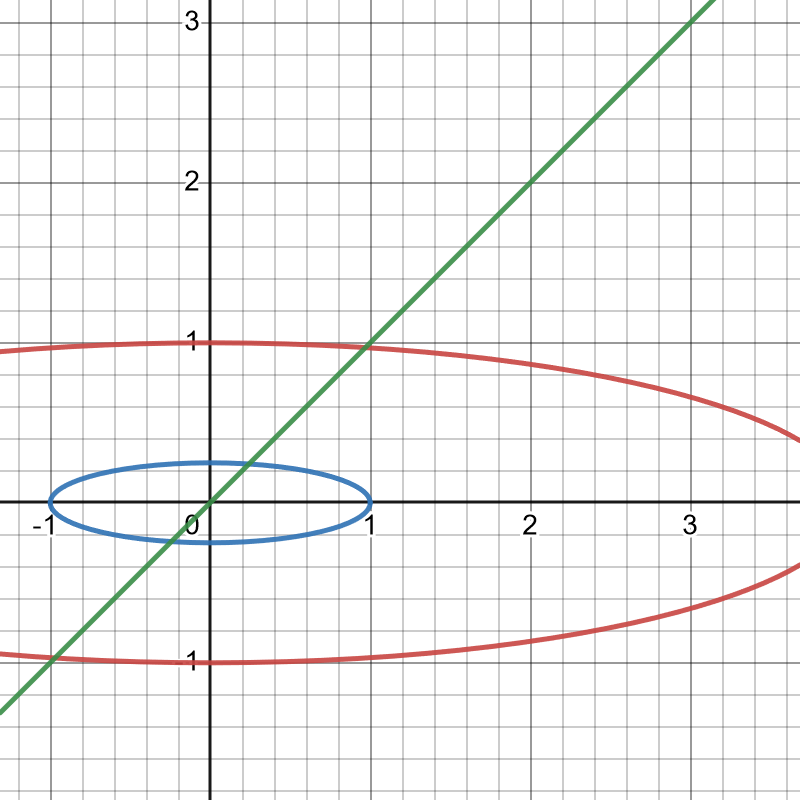
Herregud, jag inser nu att jag blandade ihop $y$ -axeln med $x$ -axeln. Om den positiva $x$ -axeln hade begränsat området hade väl $0 \leq v \leq 1$ varit rimligt?

Hursomhelst, jag inser nu mitt triviala misstag när jag låtit frågan vila en stund.

Svara