Diskret matematik: Vad är innebörden av maximala element, maximum, minimum, största...?
Hej!
Jag blir rätt så förvirrad på innebörden av vad följande termer innebär:
- Maximalt element
- Minimalt element
- Maximum/största element
- Minimum/minsta element
Det jag tror de betyder är:
- Maximalt element: om alla objekt i den delmängd du undersökt relationen på relateras till ett visst element, är det maximalt. Det kan finnas flera maximala element.
- Största element: Om det finns flera maximala element, är det största elementet det största elementet av de maximala elementen. Om de alla är lika stora finns inga maximala element. Om det bara finns ett maximalt element är det det som är störst.
- Minimalt element: Om det finns något eller några element som inte relaterar till något annat än sig själv, är de minimala element.
- Minsta element: Om det finns flera minimala element, är det minsta elementet det minsta elementet av de minimala elementen. Om de alla är lika stora finns inga minimalt element. Om det bara finns ett minimalt element är det det som är störst.
Jag hänger inte riktigt med på definitionerna som finns online.
Jag blir extra förvirrad eftersom bildtexten till denna bild på Wikipedia säger detta:
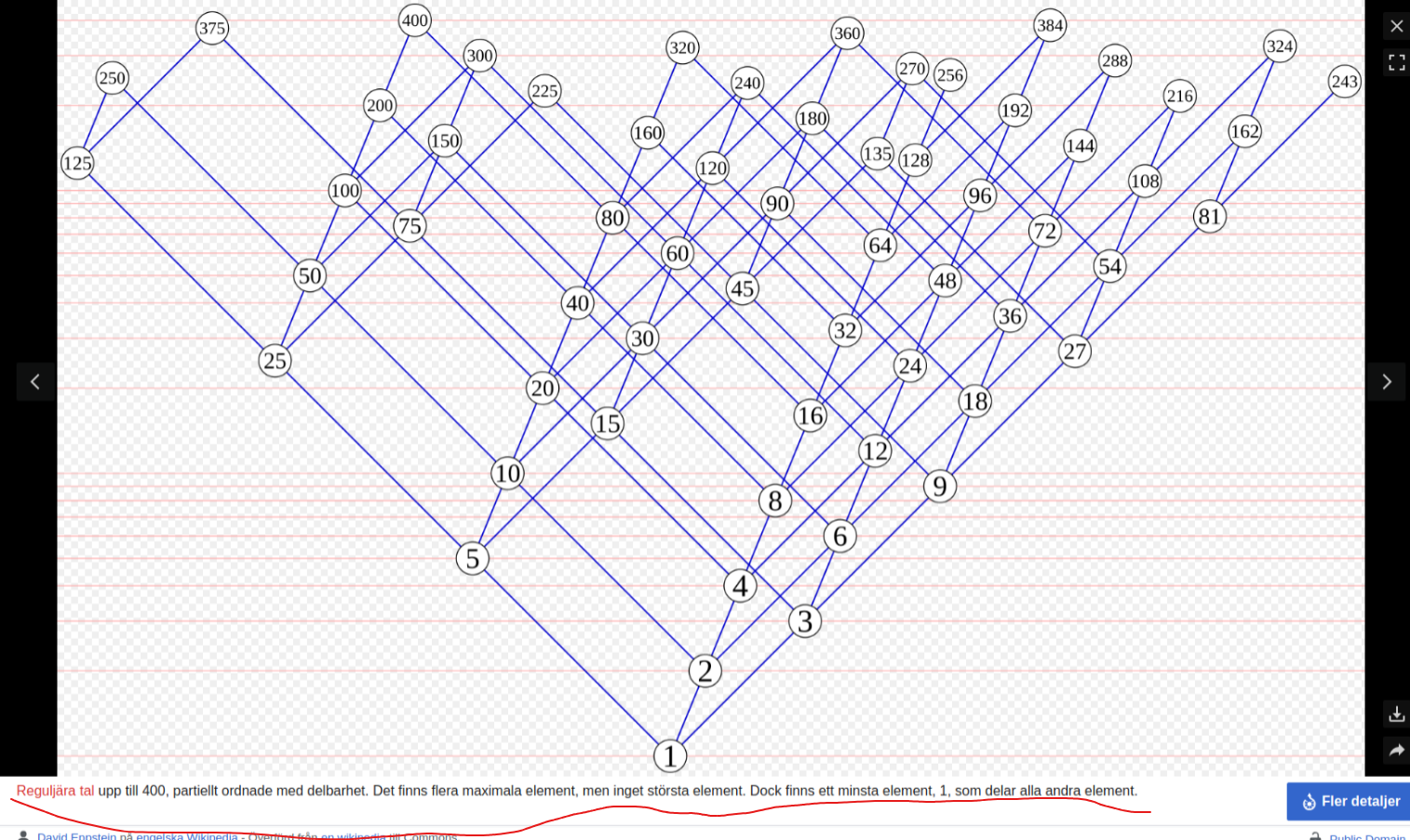
Se artikeln https://sv.wikipedia.org/wiki/Partialordnad_m%C3%A4ngd#.
Tycker du att definitionerna i wikipedia inte stämmer, eller är svårbegripliga, när man tittar på bilden? (Jag har inte läst dem än.)
Laguna skrev:Tycker du att definitionerna i wikipedia inte stämmer, eller är svårbegripliga, när man tittar på bilden? (Jag har inte läst dem än.)
Svårbegripliga, huruvida de är korrekta eller inte kan jag inte avgöra eftersom jag inte själv vet vad som är rätt eller inte. Jag kan exempelvis inte förstå varför det finns flera maximala element. Om maximalt betyder att det finns element som alla andra element relaterar till - men det relaterar enbart till sig själv - Finns det ens ett sådant? Jag ser inte det om jag tittar längst upp i grafen men kanske tänker fel.
Och om det finns ”flera maximala element” som i att alla andra element relaterar elementen, borde väl det största finnas och vara den största numeriskt sett? (t.ex. 123>99)
Det kan finnas flera maximala element. Ett sådant har inga element som är större. Du kan jämföra dem med bergstoppar, det går inte att komma högre från dem.
Med "stämmer" menade jag stämmer med bilden, eller att du inte kan formulera något som är fel med definitionerna, inte att du går i god för att de är korrekta.
Ett element som är större än alla andra element kallas största element (tydligen, jag har inte använt de svenska termerna mycket). Det finns inget sådant i bilden. Däremot finns det ett minsta, nämligen 1.
Laguna skrev:Det kan finnas flera maximala element. Ett sådant har inga element som är större. Du kan jämföra dem med bergstoppar, det går inte att komma högre från dem.
Med "stämmer" menade jag stämmer med bilden, eller att du inte kan formulera något som är fel med definitionerna, inte att du går i god för att de är korrekta.
Ett element som är större än alla andra element kallas största element (tydligen, jag har inte använt de svenska termerna mycket). Det finns inget sådant i bilden. Däremot finns det ett minsta, nämligen 1.
Jag hittar också bara engelskt material så kanske är att de svenska termerna förvirrar mig. Jag förstår inte varför det största elementet (i bilden) inte är 440? Är det enbart om det finns ett maximalt element som det finns en största element då, implicit?
Jag trodde även att ett maximalt element skulle vara relaterat till exakt allt annat i mängden, men så är ju inte fallet eftersom det finns flera maximala element. Bara att den inte relaterar till något element ”ovanför den”. Det hajar jag iallafall nu.
Eller kan det vara så här det är?
Ett minimalt element är ett element således att för ett antal a men det finns inget sa . Ett maximalt element är ett element där för ett antal a.
Ett största element uppfyller kravet för maximalt; **men** det är också relaterat till ALLA element, inte bara ”ett antal a”.
Ett minsta element uppfyller kravet för minimalt; **men** det är också relaterat till ALLA element, inte bara ”ett antal a”
där utläses ”a relaterat till b”
Det låter rätt, tycker jag.
Menade du 400? 400 är visserligen störst om man använder relationen "större än, som heltal betraktat", men det här är en annan relation, som har att göra med vilka tal som delar det.
Laguna skrev:Det låter rätt, tycker jag.
Menade du 400? 400 är visserligen störst om man använder relationen "större än, som heltal betraktat", men det här är en annan relation, som har att göra med vilka tal som delar det.
Jag menade 400, ja. Men tolka post #6 som att jag förstår nu, eftersom du verkar hålla med mig :)
Formuleringar på svenska av de här objekten har jag också upplevt lite knappa. Utgångspunkten är att vi har en partiell ordningsrelation < på en mängd M, dvs reflexiv, antisymmetrisk och transitiv. Här följer ett par gamla formuleringar från salig prof. Hanner som jag använt och verkar ha funkat:
"Ett MAXIMALT element i en ordnad mängd M är ett element för vilket det inte finns något större" Som du säger så kan det finnas flera maximala element.
"Ett STÖRSTA element är ett element S tillhörande M sådant att m < S för ALLA element i M. Om det finns ett största element så är det unikt". OBS att detta inte måste innebära att M är totalt ordnad, utan det räcker med att enbart elementet S är ordnat till alla övriga.
Begreppen MINIMALT och MINSTA element definieras analogt.
Tack Tomten (det var en rolig fras att säga) och tack Laguna!


