diskontinuerlig
hej.
1. vad säger oss hoppet (när vi lyfter pennan) i en graf som är diskontuerlig? alltså..
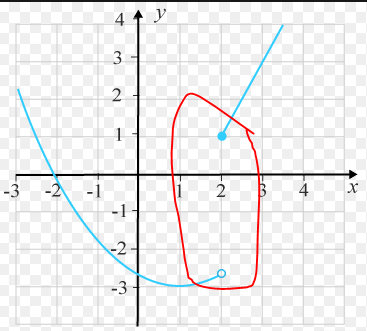
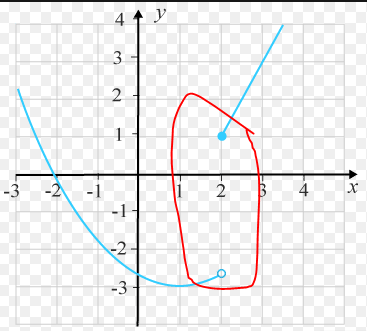
den ifyllda säger att den är större än eller lika med 2, medan den som inte är ifylld säger att den är mindre än 2,
men det jag inte förstår är,
2. varför har man "brytit" grafen, alltså varför är den itne sammanhängande?
3. och vad innebär det jag markerat inom rött?
naturnatur1 skrev:hej.
1. vad säger oss hoppet (när vi lyfter pennan) i en graf som är diskontuerlig? alltså..
den ifyllda säger att den är större än eller lika med 2, medan den som inte är ifylld säger att den är mindre än 2,
men det jag inte förstår är,
2. varför har man "brytit" grafen, alltså varför är den itne sammanhängande?
Därför att funktionen ser ut så.
Funktionen kan t.ex. vara definierad enligt följande:
- f(x) = "någon andragradfunktion" då x < 2.
- f(x) = "någon linjär funktion" då x 2
3. och vad innebär det jag markerat inom rött?
Det innebär att funktionsvärdet gör ett "hopp" vid x = 2.
Yngve skrev:
Därför att funktionen ser ut så.
Funktionen kan t.ex. vara definierad enligt följande:
- f(x) = "någon andragradfunktion" då x < 2.
- f(x) = "någon linjär funktion" då x 2
Ja men vad innebär det att den är bruten därvid? Jag förstår det är för att funktionen ser ut så och definierad så. Men VAD innebär det? alltså varför är den inte sammanhängande? vad är det som gör att det finns ett hopp däremellan?
Det innebär att funktionsvärdet gör ett "hopp" vid x = 2.
Ja, vad innebär det hoppet?
Ja men vad innebär det att den är bruten därvid? Jag förstår det är för att funktionen ser ut så och definierad så. Men VAD innebär det? alltså varför är den inte sammanhängande? vad är det som gör att det finns ett hopp däremellan?
Det betyder bara att funktionen har ett hål där. Hål och hack kan uppstå i funktioner som modellerar verkligheten, eftersom det ibland är så att värden "sticker iväg" åt något håll, när en parameter kommer över ett visst värde (ett så kallat tröskelvärde).
Hoppet innebär bara att funktionen, i just punkterna kring , inte är sammanhängande. Om x är nära två, men fortfarande mindre än två, går värdet av funktionen mot ca. -2,7, men om x är nära två och större än två, går värdet av funktionen mot 1.
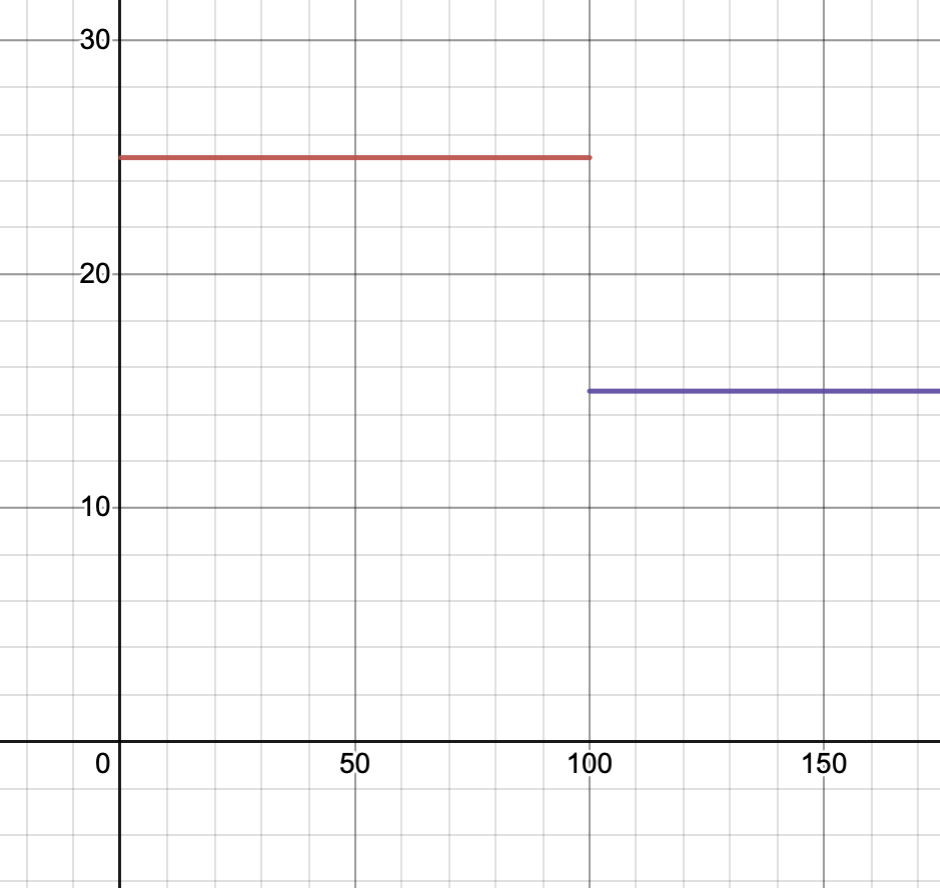
Om du modellerar kilopriset för en produkt, kan det uppstå ett hack om du får mängdrabatt. Exempelvis:
Kom och köp äpplen! För äppelinköp upp till 100 kg, är kilopriset 25 kr/kg, men om du köper över 100 kg äpplen, behöver du bara betala 15 kr/kg!
Om vi modellerar kilopriset, emot antalet kilo äpplen som köps, blir grafen:
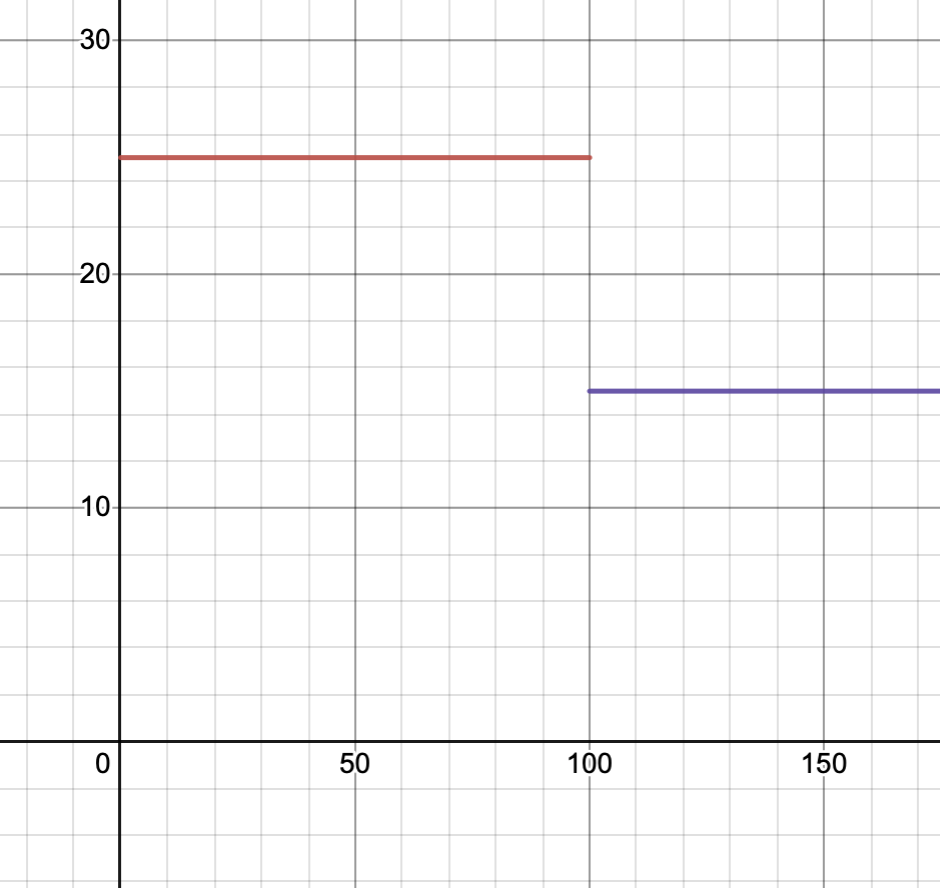
Här uppstår det ett hopp kring , eftersom priset förändras där. Det betyder inte mer än så. :)
Smutstvätt skrev:Ja men vad innebär det att den är bruten därvid? Jag förstår det är för att funktionen ser ut så och definierad så. Men VAD innebär det? alltså varför är den inte sammanhängande? vad är det som gör att det finns ett hopp däremellan?
Det betyder bara att funktionen har ett hål där. Hål och hack kan uppstå i funktioner som modellerar verkligheten, eftersom det ibland är så att värden "sticker iväg" åt något håll, när en parameter kommer över ett visst värde (ett så kallat tröskelvärde).
Hoppet innebär bara att funktionen, i just punkterna kring , inte är sammanhängande. Om x är nära två, men fortfarande mindre än två, går värdet av funktionen mot ca. -2,7, men om x är nära två och större än två, går värdet av funktionen mot 1.
Om du modellerar kilopriset för en produkt, kan det uppstå ett hack om du får mängdrabatt. Exempelvis:
Kom och köp äpplen! För äppelinköp upp till 100 kg, är kilopriset 25 kr/kg, men om du köper över 100 kg äpplen, behöver du bara betala 15 kr/kg!
Om vi modellerar kilopriset, emot antalet kilo äpplen som köps, blir grafen:
Här uppstår det ett hopp kring , eftersom priset förändras där. Det betyder inte mer än så. :)
Tack så mycket för din förklaring, exemplet gjorde det mycket tydligare!
Jag och Yngve hälsar varsågod! :)
(@Yngve: Jag tar mig friheten att "varsågod-a" åt dig 😅😊)
Smutstvätt skrev:Jag och Yngve hälsar varsågod! :)
(@Yngve: Jag tar mig friheten att "varsågod-a" åt dig 😅😊)
ni är grymma :)