Differentierbar medför kontinuitet?
Om vi har en funktion som är differentierbar i (a,b) varför är den då kontinuerlig i (a,b)?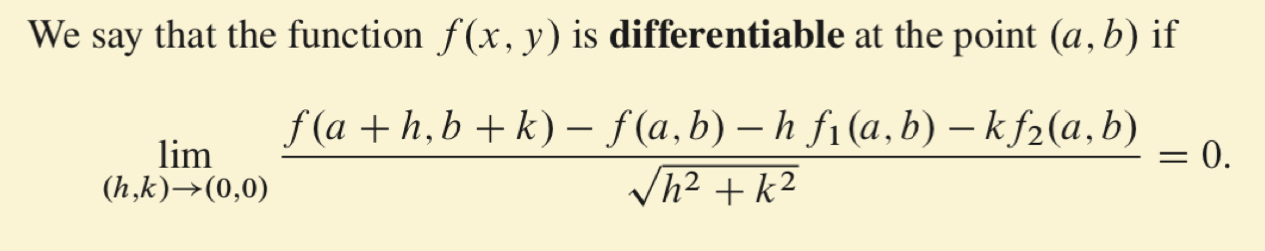 
Man vet sen tidigare att trots att de partiella derivatorna existerar så betyder det inte nödvändigtvis att funktionen är kontinuerlig. Så varför kan inte fallet vara så nu, dvs att funktionen inte är kontinuerlig men att de partiella derivatorna existerar.
Litet ostringent här, men hf1 och kf2 går ju mot noll så f(a+h, b+k) – f(a, b) måste också gå mot noll eftersom nämnaren gör det.
Mogens skrev:Litet ostringent här, men hf1 och kf2 går ju mot noll så f(a+h, b+k) – f(a, b) måste också gå mot noll eftersom nämnaren gör det.
?
Ja, gränsvärden handlar ofta om att både täljare och nämnare går mot noll, och så studerar man vart kvoten tar vägen.
Du verkar läsa en kurs i flervariabelanalys, har du inte läst om gränsvärden i en envariabelkurs?
T ex
x2/x
när x är 0 är kvoten inte definierad.
när x är skilt från 0 så är kvoten = x som går mot 0 när x går mot 0. Så x2/x går mot 0 när x går 0.
Men betraktar du x/x så går det mot 1 när x går mot 0.
Mogens skrev:T ex
x2/x
när x är 0 är kvoten inte definierad.
när x är skilt från 0 så är kvoten = x som går mot 0 när x går mot 0. Så x2/x går mot 0 när x går 0.Men betraktar du x/x så går det mot 1 när x går mot 0.
Ja det är jag med på. Men du förenklar ju inte uttrycket för differentierbarhet på samma sätt.
Du har tre olika begrepp i din fråga, och det är väldigt viktigt att inte blanda ihop dem
- Partiella derivator
- Differentierbarhet
- Kontinuerlig
Det gäller att en differentierbar funktion är kontinuerlig.
Det gäller också att en differentierbar funktion är partiellt deriverbar.
Men det gäller INTE en partiellt deriverbar funktion är kontinuerlig. Därmed gäller inte heller att en partiellt deriverbar funktion är differentierbar.
Man säger att differentierbarhet är ett strängare krav än partiell deriverbarhet.
För att ytterligare förvirra läsaren noterar vi följande:
Om de partiella derivatorna 1) existerar och dessutom är 2) kontinuerliga på den öppna definitionsmängden för så kan man dra slutsatsen att funktionen är differentierbar.
D4NIEL skrev:Du har tre olika begrepp i din fråga, och det är väldigt viktigt att inte blanda ihop dem
- Partiella derivator
- Differentierbarhet
- Kontinuerlig
Det gäller att en differentierbar funktion är kontinuerlig.
Det gäller också att en differentierbar funktion är partiellt deriverbar.
Men det gäller INTE en partiellt deriverbar funktion är kontinuerlig. Därmed gäller inte heller att en partiellt deriverbar funktion är differentierbar.
Man säger att differentierbarhet är ett strängare krav än partiell deriverbarhet.
För att ytterligare förvirra läsaren noterar vi följande:
Om de partiella derivatorna 1) existerar och dessutom är 2) kontinuerliga på den öppna definitionsmängden för så kan man dra slutsatsen att funktionen är differentierbar.
Tack ska du ha för en mycket bra sammanfattning!
Ja, bra sammanfattning.
Tänk dig spetsen av en konformad graf. Funktionen är kontinuerlig men saknar partiella derivator i punkten,
Tänk dig sedan f(x, y) = 0 överallt utom längs x-axeln och y-axeln där f = 1. Den är inte kontinuerlig i origo men har partiella derivator där.
