Differentialekvation med integrerande faktor
Jag ska lösa följade uppgift med integrerande faktor:
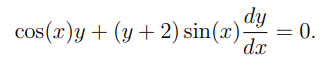
Jag har förstått att jag behöver hitta en integrerande faktor μ(x) så att , men kommer inte längre än så. Uppskattar hjälp!
Hej!
Jag tycker att den ser ut att vara separabel.
Ja, absolut! Känns ju mycket enklare att lösa den på det viset. Grejen är bara att det står i uppgiften att den måste lösas med integrerande faktor... (tyvärr :) )
Kan du ta bild på uppgiftsbeskrivningen, och ev om det finns ex i boken/föreläsningen där en liknande uppgift är löst på det sättet? Vilken kurs hör det här till?
Detta är inte integrerande faktor som den normalt är känd. I detta fall gör man en inexakt ekvation på formen exakt genom en integrerande faktor så att den blir separabel:
Vi har:
Vi ser att varför detta är en inexakt differentialekvation. Vi formulerar därför:
Vi har nu en integrerande faktor som:
Tillägg: 5 jan 2022 11:06
Notera att poängen med integrerande faktor är att vi helst vill ha den som funktion av antingen eller , inte båda. Detta därför att vi annars måste lösa en PDE vilket undanbedes till förmån för ODE.
Alltså, när jag formulerar
kontrollerar jag om resultatet är en funktion av endast . Om inte, kan jag formulera
och kontrollera om detta är en funktion av endast .
Tillägg: 5 jan 2022 17:06
Jag såg nu att jag räknat fel på integranden för faktorn, den ska vara:
Jag får ursäkta.
Det funkar ju, häftigt! Heter den här metoden nånting?
Och vad vann man på den? Ekvationen var ju separabel från början, så det är bara samma ekvation man får fram som om den lösts så från början? 🤔
Det har tillämpning inom ingenjörsteknik och fysik då du tvingar fram en exakt ekvation som du i många fall exempelvis kan formulera en potentialfunktion för:
https://en.wikipedia.org/wiki/Exact_differential_equation
En exakt differentialekvation har helt enkelt många bra egenskaper. Dessutom är lösningen enkel och snabb samt implicit (vilket vi alltid gillar) jämfört med traditionell lösning som är explicit och kan vara omständlig. Läs mer här om varför:
https://tutorial.math.lamar.edu/classes/de/exact.aspx
Tillägg: 5 jan 2022 12:23
Ha i åtanke att det var tre år sedan jag läste om detta och jag är ingen matematiker så exakta detaljerna får du söka annorstädes :]




