Differentialekvation - Envariabelsanayls 2
Jag har följande differentialekvation: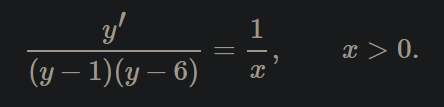
Där en tidigare deluppgift var att ta fram primitiven till:
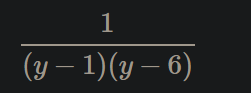Vilket leder in på själva frågan jag inte vet hur jag ska lösa...
Ledningen till frågan är: "En primitiv med avseende på 'x' till högerledet 1/x som fungerar i alla möjliga delintervall för x är ju ln|x|, men här är x>0, så integration av differentialekvationen ger i så förenklad form som möjligt: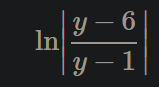
=...?
Min tanke är att ta fram primitiven till det som står ovan, och sedan förenkla det: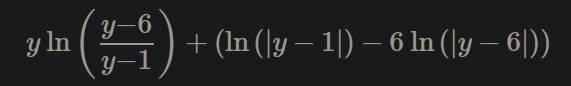
Och får då detta, vilket dock inte verkar vara rätt svar till frågan...? Har jag tolkat uppgiften fel kanske?
Tack!
Jag gissar att de använder sig av kedjeregeln: derivatan av f(y(x)) = f'(y)*y'(x). Vi ser att täljaren i VL är y'(x) och resterande faktor blir därmed f'(y). Eftersom att du har bestämt den primitiva funktionen av denna har du f(y) som blir lika med ln(x) (primitiva funktionen av HL).
