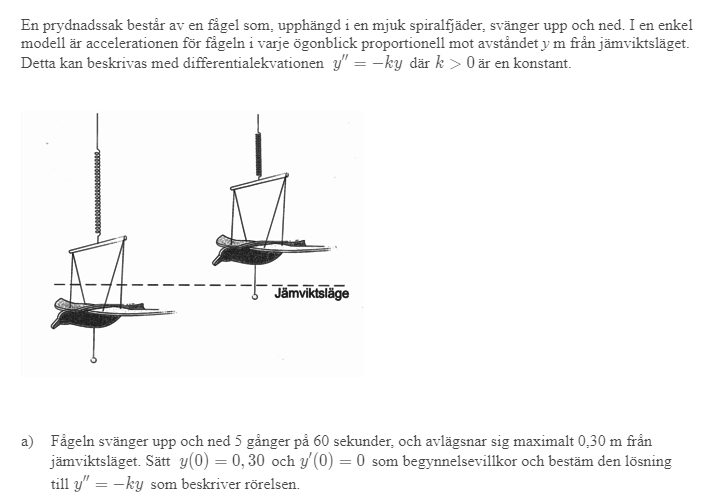
Differentialekvation av andra ordningen
Facit: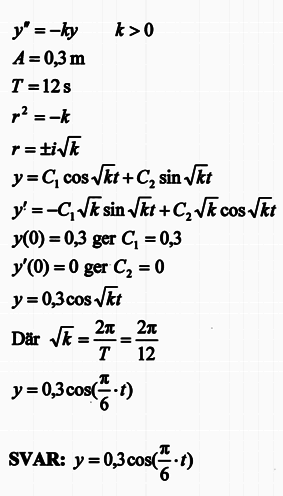 Varför är k^(1/2) = 2pi/T ?
Varför är k^(1/2) = 2pi/T ?
Eftersom den svängerupp och ned 5 gånger på 60 sekunder svänger det en gång på 12 sekunder. T = 12. Perioden för cos t är 2pi.
För att synka cosinusfunktionen till svängningen måste vi ha cos [(2pi/T)t].
Så egentligen kan man fråga sig varför vi behöver lösa diffekv med kar ekv etc. Kanske för att man ska inse att svängningen inte dämpas.
Eller inse att cos t och sin t båda är lösningar till diffekv y’’ = –y.
I vissa sammanhang definierar man funktionen y = sin(t) som lösningen till
y’’ = –y ; y(0) = 0.
och y = cos(t) som y’’ = –y ; y(0) = 1.
På samma sätt som man kan definiera y = ex som lösn till ekv
y’ = y; y(0) = 1
(och e som y(1).)
Marilyn skrev:Eftersom den svängerupp och ned 5 gånger på 60 sekunder svänger det en gång på 12 sekunder. T = 12. Perioden för cos t är 2pi.
För att synka cosinusfunktionen till svängningen måste vi ha cos [(2pi/T)t].
Så egentligen kan man fråga sig varför vi behöver lösa diffekv med kar ekv etc. Kanske för att man ska inse att svängningen inte dämpas.
Eller inse att cos t och sin t båda är lösningar till diffekv y’’ = –y.
I vissa sammanhang definierar man funktionen y = sin(t) som lösningen till
y’’ = –y ; y(0) = 0.
och y = cos(t) som y’’ = –y ; y(0) = 1.
På samma sätt som man kan definiera y = ex som lösn till ekv
y’ = y; y(0) = 1
(och e som y(1).)
Tack!

