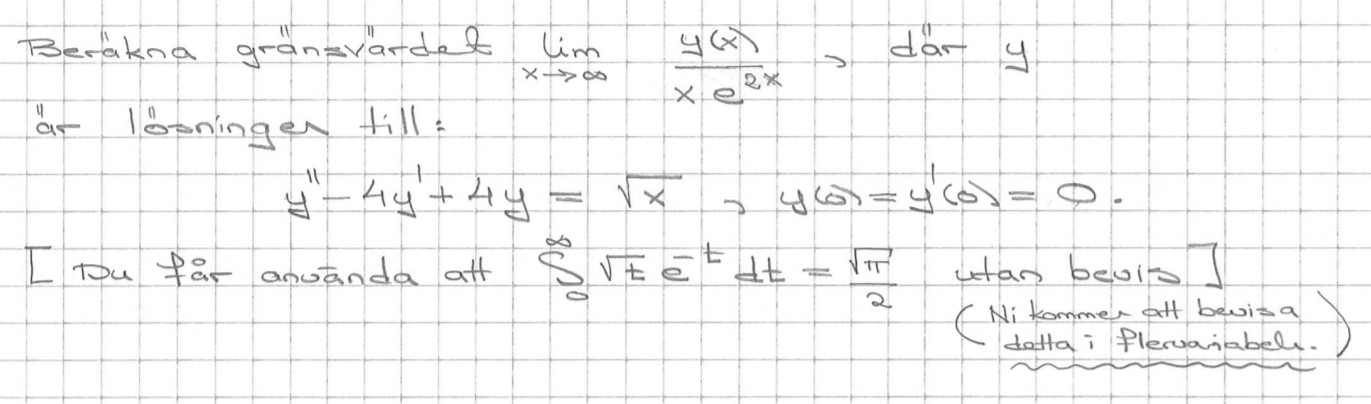Differentialekvaiton
Hej!
Jag har fastnat vid försök av lösning av differentialekvation som ni finner i länken nedan.
https://gyazo.com/d12242f317352d4c0b6b771d9fc60ed1
Mitt försök:
https://gyazo.com/85fb23f81fbeab39239734d659ec1a3e
Problem: Integralen i slutet, dels så vet jag inte hur man integrerar den, dels kommer jag och tänka på om huruvida jag bör har den integralen där och inte den givna i uppgiften?
Tack på förhand.
Om du sätter t=2x och byter ut variablerna borde du kunna faktorisera ut konstanter så att du får den givna integralen
Har lite svårt att följa med i din lösning.
Jag skulle först notera att vi kan skriva ekvationen som
, där D är deriveringsoperatorn.
Min idé är nu att utnyttja förskjutningsregeln och gör därför ansatsen
, så att
, och således får vi följande ekvation för u
.
Integration och begynnelsevillkor ger
Ytterligare en integration och begynnelsevillkor ger
Notera att
.
= + - = .
Visa spoiler
Skriv ditt dolda innehåll här
PATENTERAMERA skrev:
Har lite svårt att följa med i din lösning.
Jag skulle först notera att vi kan skriva ekvationen som
, där D är deriveringsoperatorn.
Min idé är nu att utnyttja förskjutningsregeln och gör därför ansatsen
, så att
, och således får vi följande ekvation för u
.
Integration och begynnelsevillkor ger
Ytterligare en integration och begynnelsevillkor ger
Notera att
.
= + - = .
 Hur kan detta gälla? Du gjorde dig ju av med två termer, -4y' och 4y? Jag har inte lärt mig förskjutningsregeln på ditt sätt utan såsom jag använder den i bilden, då ser man att ekvationerna är samma.
Hur kan detta gälla? Du gjorde dig ju av med två termer, -4y' och 4y? Jag har inte lärt mig förskjutningsregeln på ditt sätt utan såsom jag använder den i bilden, då ser man att ekvationerna är samma.
blygummi skrev:Visa spoiler
Skriv ditt dolda innehåll här
PATENTERAMERA skrev:
Har lite svårt att följa med i din lösning.
Jag skulle först notera att vi kan skriva ekvationen som
, där D är deriveringsoperatorn.
Min idé är nu att utnyttja förskjutningsregeln och gör därför ansatsen
, så att
, och således får vi följande ekvation för u
.
Integration och begynnelsevillkor ger
Ytterligare en integration och begynnelsevillkor ger
Notera att
.
= + - = .
Hur kan detta gälla? Du gjorde dig ju av med två termer, -4y' och 4y? Jag har inte lärt mig förskjutningsregeln på ditt sätt utan såsom jag använder den i bilden, då ser man att ekvationerna är samma.
Om p(D) är ett polynom i deriveringsoperatorn D, så säger förskjutningsregeln att
.
Du kan bevisa detta genom att beakta och använda induktion. Eller googla.
PATENTERAMERA skrev:blygummi skrev:Visa spoiler
Skriv ditt dolda innehåll här
PATENTERAMERA skrev:
Har lite svårt att följa med i din lösning.
Jag skulle först notera att vi kan skriva ekvationen som
, där D är deriveringsoperatorn.
Min idé är nu att utnyttja förskjutningsregeln och gör därför ansatsen
, så att
, och således får vi följande ekvation för u
.
Integration och begynnelsevillkor ger
Ytterligare en integration och begynnelsevillkor ger
Notera att
.
= + - = .
Hur kan detta gälla? Du gjorde dig ju av med två termer, -4y' och 4y? Jag har inte lärt mig förskjutningsregeln på ditt sätt utan såsom jag använder den i bilden, då ser man att ekvationerna är samma.
Om p(D) är ett polynom i deriveringsoperatorn D, så säger förskjutningsregeln att
.
Du kan bevisa detta genom att beakta och använda induktion. Eller googla.
Eller så gör jag som föreläsaren sagt att vi ska göra i uppgiften, använda hans sätt att uttrycka förskjutningsregeln, såsom jag gjort. 
Finns dock ett problem, jag förstår inte vissa delsteg. Jag skulle vilja påstå att jag förstår allt till och med "Obs".. gränsvärdet av f(t) då t går mot oändligheten är lika med ... Och så vidare. Jag förstår uträkningen i sig, dock inte varför gränsvärdet då t går mot oändligheten är LIKA MED integralen av f(t), från noll till oändligheten!
Min tanke: Om jag utför denna integralen:
Alltså, integralen är lika med funktionsvärdet vid x. På något sätt vill jag blanda in gränsvärdet i uttrycket nu men ser inte riktigt hur.

Sen ser fjärde pilen konstig ut, jag förstår inte alls vad som händer, kanske lag till och tog bort gränsvärdet? Kan man då bara lägga det i integralen sådär? När vi väl har uttrycket som kommer efter fjärde pilen (räknat från första bilden) förstår jag inte hur det kan vara större eller lika med än samma sak adderat med en positivt konstant? Exempelvis, hur kan: 4+2 < 4? Sen verkar det som att han säger att det som är kvar i integralen går mot noll, vilket heller inte är klart för mig, summan av integralen med endast f(t) i subtraherat med gränsvärdet då t-> oändligheten går mot noll, om det i bilden ovan gör det är oklart.
Tror du att du kan hjälpa mig förstå detta?
Är du med så långt att
= , där ?
Vidare är du antagligen med på att
.
Vi har därför att
= - = .
Vidare så är du säkert med på att
, då . Så om t så har vi
.
Vidare så har vi nu att
.
Resten av beviset går ut på att visa att
, vilket implicerar att
. Jag tror du kan följa den delen av beviset själv med vad sagts ovan.