Diagonalisering av 3x3 matris
Hej
Jag har generellt väldigt svårt att lösa uppgifter som i fråga B, där frågan är "avgör om matrisen är diagonaliserbar. Jag vet att steg 1 är att hitta egenvärden/egenvektorer, men med varje uppgift blir uträkningen för determinanten väldigt lång och klumpig. Jag förstår inte hur jag ska beräkna determinanten på ett enkelt sätt så att det blir rätt. Jag bifogar min uträkning, det enda jag får fram är en lång ekvation som jag inte får fram egenvärdena på. vad är det jag gör fel/kan förbättra för att pricksäkert kunna lösa liknande uppgifter? (Edit: jag ser att jag räknade fel i sista systemet -6+8=2, så utöver det tycker jag allt bör stämma)
Vad fick du fram på a? Jag tycker att v inte är en egenvektor, men däremot w. Då har du ett nollställe och kan få fram de övriga.
Men stämmer din determinant?
På a fick jag fram att V inte är en egenvektor precis som du säger. Vad innebär det att jag har ett nollställe? Hur hänger vektorn v ihop med matrisen A om den inte är en egenvektor till A?
Det är det jag undrar, jag kofaktorutvecklade (tror jag..) längst rad 1.
Det är rätt ganska långt, men nånting händer på slutet. -6+8 = 2, och varför blev det -3 framför ?
Jag insåg att jag hade gjort misstaget att -6+8 blev -14 istället för 2. Nu ser jag båda felen. Tack!
Men isåfall blir ekvationen väl -λ3+4λ2-5λ+2. Men efter detta vet jag inte vad jag ska göra för att få fram egenvärdena. Ekvationen kan faktoriseras genom att bryta ut lambda så λ (-λ2+4λ-5)+2. Men jag vet ändå inte hur jag ska göra efter det
Man kan hoppas på att det finns heltalsrötter, och i så fall är de delare till konstanttermen 2.
Jag fick ju också för mig att prova om w är en egenvektor. Om den är det så får du ett egenvärde den vägen.
Får inte fram heltalsrötter vilket får mig tro att något i min uträkning inte stämmer. I facit har de inte sagt något om att använda v eller w, de har ställt upp determinanten och fått egenvärdena därifrån. Dock ser facits determinant ut på detta vis:
det(𝐴−𝜆𝐼) = (2−𝜆)((3−𝜆)(−1−𝜆)+4) = (2−𝜆)(𝜆−1)2
vilket inte alls är hur min ser ut... förstår inte vart det går snett.
(2-L)((L-1)2 = (2-L)(L2-2L+1) = 2L2-4L+2-L3+2L2-L = -L3+4L2-5L+2, och det är ju ditt uttryck. Jag skrev L för att jag var lat.
det har du visst rätt i! tack.
Det jag inte fattar är fortfarande hur jag ska kunna förenkla så långa uttryck för att smidigt kunna hitta egenvärdena? Utifrån min icke förenklade ekvation fanns det inte ens heltalsrötter
Dimatt skrev:Får inte fram heltalsrötter vilket får mig tro att något i min uträkning inte stämmer. I facit har de inte sagt något om att använda v eller w, de har ställt upp determinanten och fått egenvärdena därifrån. Dock ser facits determinant ut på detta vis:
det(𝐴−𝜆𝐼) = (2−𝜆)((3−𝜆)(−1−𝜆)+4) = (2−𝜆)(𝜆−1)2
vilket inte alls är hur min ser ut... förstår inte vart det går snett.
Prova att utveckla längs med sista kolumnen istället’
Otroligt att jag inte såg det från början, tusen tack för all hjälp!
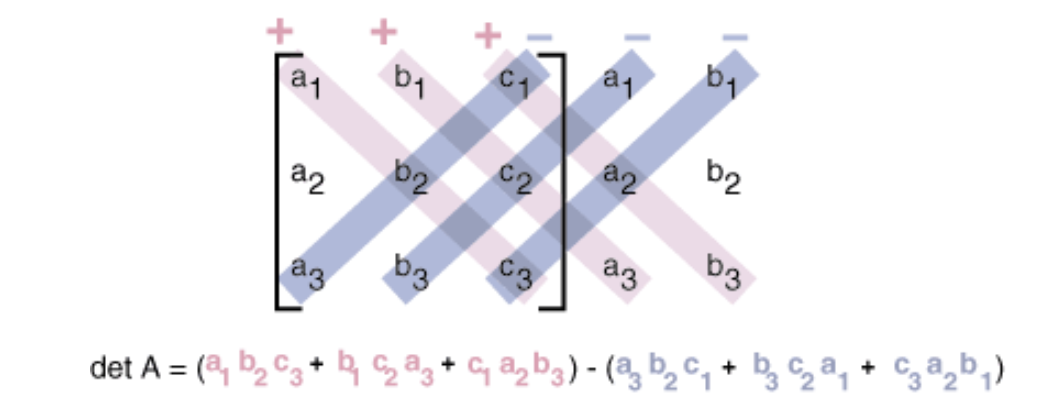Denna minnesregel för att beräkna determinant hos 3x3or är också ett alternativ.
