Diagonal

Rita en figur.

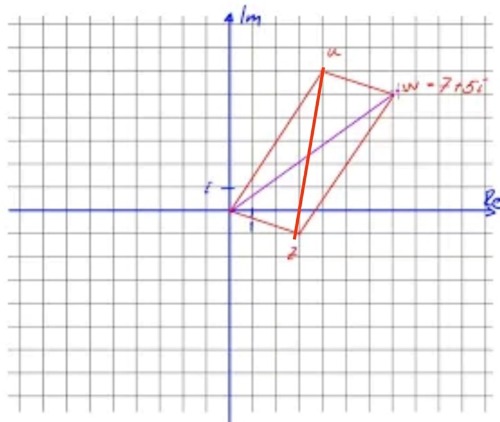
Det är inte min bild. Men jag har gjort en liknande. Jag är ute efter den röda linjen. 

Tillägg: 2 dec 2023 21:13

Pythagoras funkar nog. Men vill även kunna lösa det mha det komplexa talplanet.

Tillägg: 2 dec 2023 21:20

Nej kom på att det är en parallelogram och därför funkar det inte med pythagoras. Hur gör man annars?

enklast är nog att använda avståndsformeln.

$\sqrt{{(3-4)}^2+{(-1-6)}^2}$

om du vill använda komplexa tal: vad blir u-z ?

Ture skrev:

enklast är nog att använda avståndsformeln.

$\sqrt{{(3-4)}^2+{(-1-6)}^2}$

om du vill använda komplexa tal: vad blir u-z ?

Tack då är jag med.

Men hur kommer det sig att I u-z I ger sträckan av den diagonalen? Förstår att det innebär en längd på en vektor, men varför just u -z?

Som du var inne på, se det som 2 vektore, du ka lika väl ta beloppet av z - u. Prova! 

Ture skrev:

Som du var inne på, se det som 2 vektore, du ka lika väl ta beloppet av z - u. Prova! 

Hur kan en differens av u och z och även en addition av u och z båda resultera i en längd på en diagonal inom samma parallelogram?

|u-z| =|z-u|, men |z+u| är något annat (men lika med |u+z|).

naturnatur1 skrev:

Ture skrev:

Som du var inne på, se det som 2 vektore, du ka lika väl ta beloppet av z - u. Prova! 

Hur kan en differens av u och z och även en addition av u och z båda resultera i en längd på en diagonal inom samma parallelogram?

Rita och utför vektoraddition och vektorsubtraktionen grafiskt så blir det enklare att förstå hur det hänger ihop.

OM du inte kommer ihåg hur man gör kan du kolla här:

https://www.matteboken.se/lektioner/matte-1/geometri/rakna-med-vektorer#!/