Det gäller att cos ( 3 6 ∘ ) ≈ 0 , 809 cos Använd sambandet för att lösa ut cos3x=0.809
Det gäller att cos(36∘)≈0,809cos(36∘)≈0,809.
Använd detta för att bestämma alla lösningar till ekvationen
cos(3x)=0,809cos
Jag kom fran till positiv 12 , men i svaret ska det vara både positiv och negativ 12 och inom perioden n *120grader . Varför just perioden 120 grader och varför även negativ 12? Jag försökte klura ut det med en enhetscirkel men kom ingen vart.
Om du kollar på enhetscirkeln så kan du se att
cos x = cos -x
cosinus har perioden 360 grader, när du sedan löser ut 3:an ur vänsterledet får du 360\3 vilket ger 120 grader.
hängde du med?
jag hänger med dock säger facit 150 grader 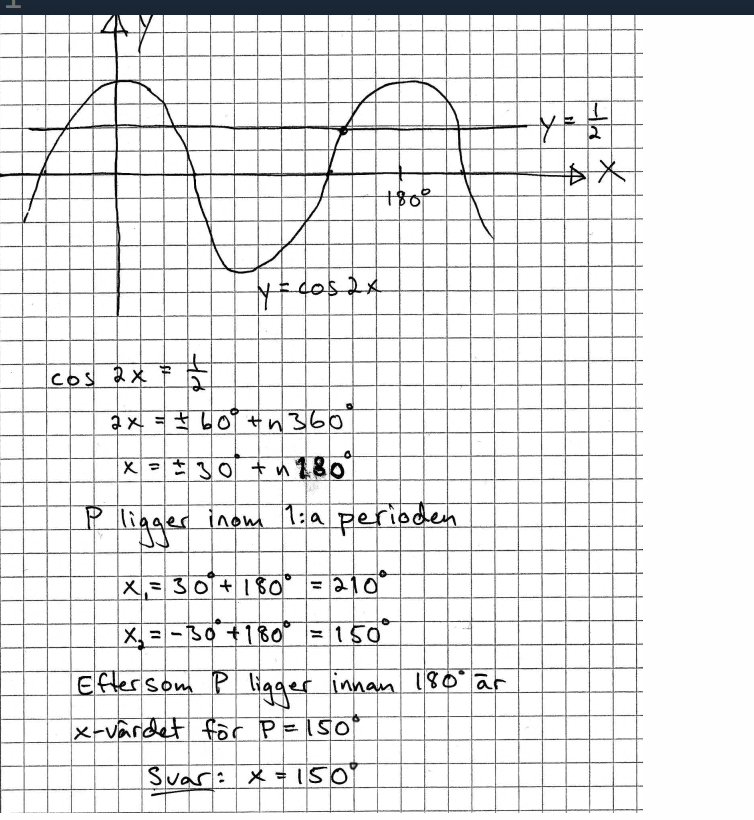
jag hänger inte riktigt med här
Det du visade nu var en annan uppgift, men tankesättet går ändå att använda.
För alla vinklar v gäller det att cos(v) = cos(-v).
Det betyder att alla ekvationer cos(v) = någonting har två lösningar (plus n*360°).
En av dessa befinner sig i övre halvplanet och en av dessa befinner sig i nedre halvklotet.
Dvs cos(v) = a har lösningarna v = arccos(a) + n*360°.
Är du med så långt?
Tack så mycket jag insåg att det var två olika uppgifter nu också


