deriverings regler

jag deriverar 3x^2/2 =får det till 6x/2 förenklar till 3x

på 2/x * (3-rot-x) ska jag dela upp den och derivera x med 2 och låta 3-rot deriveras med 1 alltså att jag bryter ut den 2/x * 1/3-rot-x eller kan jag multiplicera x en med varandra sedan derivera ?

2x = 2

rot X = x^1/2 = 1/2x^-1/2

=3x-2/x^2 * -1/3x^4/3 + 2 * 1/1x^1/2 <-- stämmer det här för känns lite konstigt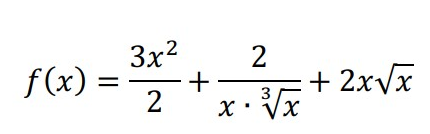

Hej.

Jag förstår inte riktigt vad du menar.

Det finns ett par räkneregler du kan använda här:

Om f(x) är en summa av termer så är f'(x) lika med summan av termernas derivator, dvs du kan derivera termerna var för sig.
Med hjälp av potenslagen $\sqrt[a]{b}=b^{\frac{1}{a}}$ så kan du skriva om den sista termen och nämnaren i mittentermen.
Med hjälp av potenslagen $a^b\cdot a^c=a^{b+c}$ så kan du skriva om den sista termen och nämnaren i mittentermen ytterligare.
Med hjälp av potenslagen $a^{-b}=\frac{1}{a^b}$ så kan du skriva om mittentermen till något som är enklare att derivera.

ska undersöka tack

Yngve skrev:
Hej.

Jag förstår inte riktigt vad du menar.

Det finns ett par räkneregler du kan använda här:

Om f(x) är en summa av termer så är f'(x) lika med summan av termernas derivator, dvs du kan derivera termerna var för sig.

Med hjälp av potenslagen $\sqrt[a]{b}=b^{\frac{1}{a}}$ så kan du skriva om den sista termen och nämnaren i mittentermen.

Med hjälp av potenslagen $a^b\cdot a^c=a^{b+c}$ så kan du skriva om den sista termen och nämnaren i mittentermen ytterligare.

Med hjälp av potenslagen $a^{-b}=\frac{1}{a^b}$ så kan du skriva om mittentermen till något som är enklare att derivera.

kan det här stämma ?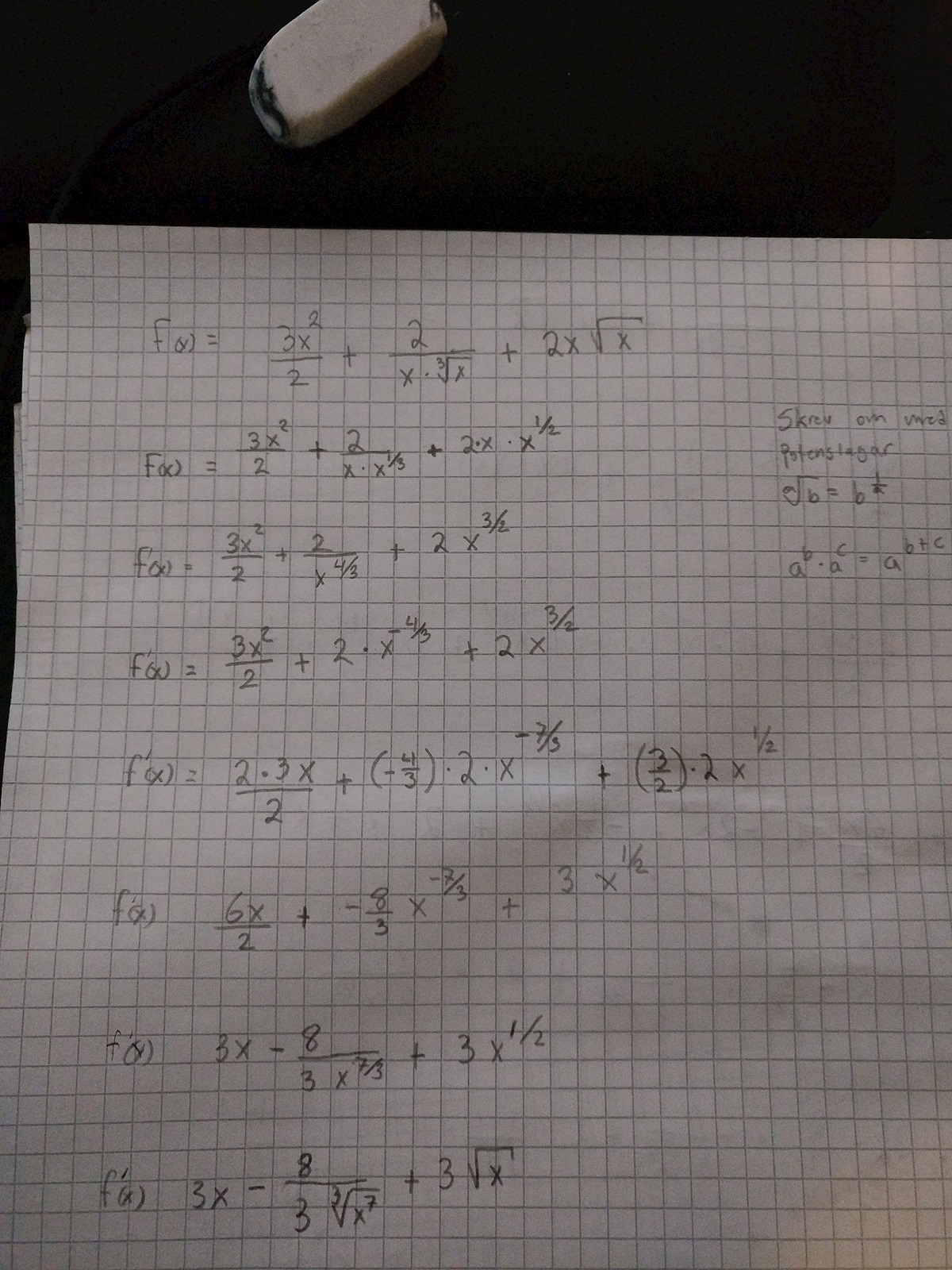

Ja det är.rätt.

Men du bör nog skriva om mittentermens nämnare till $3x^2\sqrt[3]{x}$ .

Yngve skrev:
Ja det är.rätt.

Men du bör nog skriva om mittentermens nämnare till $3x^2\sqrt[3]{x}$ .

tack så mycket för hjälpen <3 god jul på dig

Svara

Visa senaste svar