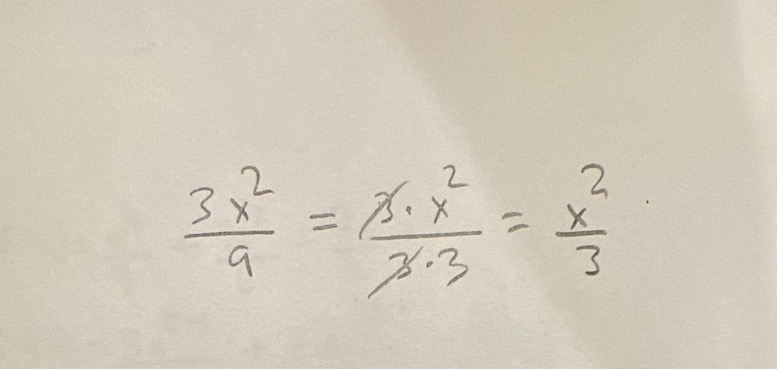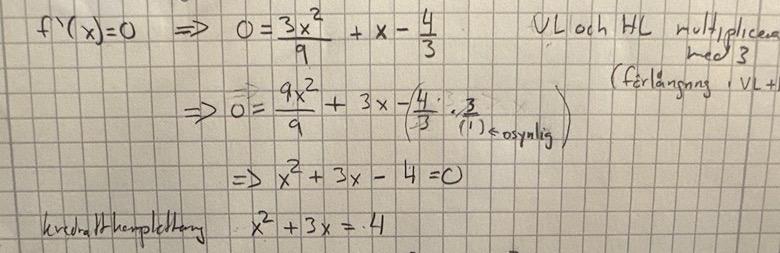Derivering

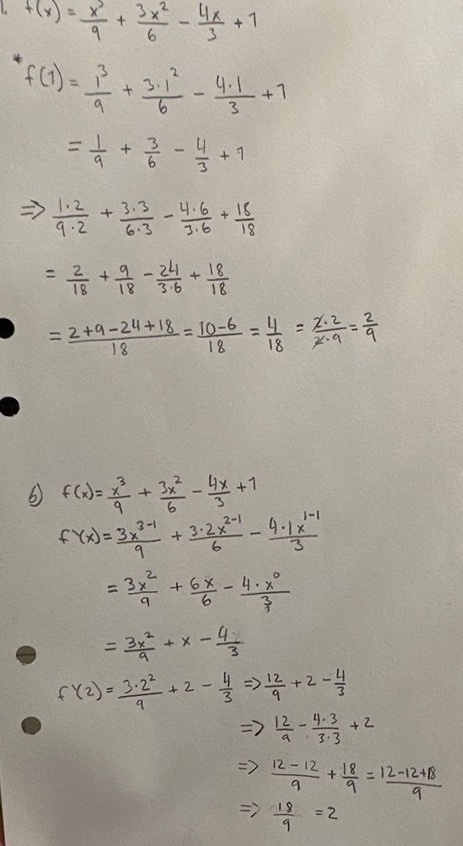
a) 2+9-24+18=5

$\frac{5}{18} = 0,277 777 ...$

b) Skriv lite kortare

$\left(\frac{x^3}{9}+\frac{3x^2}{6}-\frac{4x}{3}+1\right)\text{'}=\frac{x^2}{3}+x-\frac{4}{3}$

En del ovmvandlingar/förenklingar kan man göra i huvudet och det ska vara förståeligt för en som kan matte. Jag tycker att du är klar med formalia och kan ta ett steg fram - varför skriva $\frac{3x²}{9}$om du direkt kan skriva $\frac{x^2}{3}$?

Jag tror att du klarar det.

$f\text{'}\left(2\right) = \frac{2^2}{3}+2-\frac{4}{3}=\frac{4+6-4}{3}=2$

Bra gjort!

Med du kan ta ett kliv fram! Det kan bli fel när du försöker att ta flera steg i huvudet och man behöver hålla balansen mellan en tydlig redovisning och lagom kort redovisning, men försök! Jag tycker att du kan avancera lite mer och bli effektivare i din räkning.

Hur fick du 5/18 som svar på a)?

gjorde jag fel med minsta gemensamma nämnare?

2+9=11

18+11=29

29-24 = 5

Inget fel med MGN, bara ett litet räknefel när du räknade täljare

Så efter man deriverat så kan man utöver att identifiera MGN även förenkla bara en term i ekvationen genom 

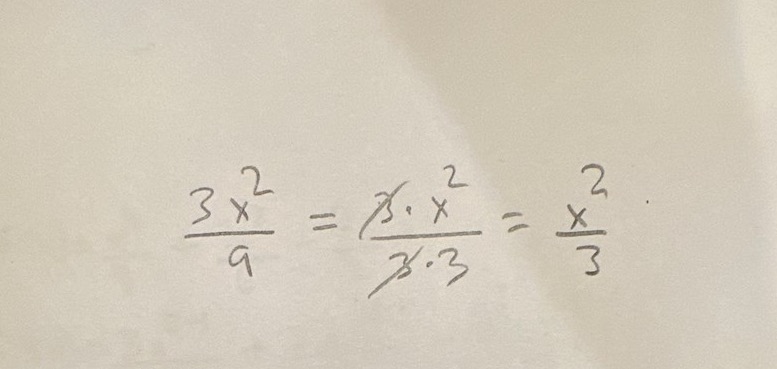
vidare på uppgift c)

så ser jag att jag kommer behöva börja med att förlänga VL och HL med 3.

innan man därefter går Vidare med kvadratkomplettering

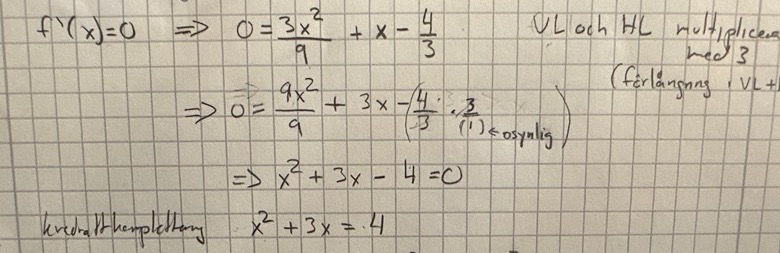
Biorr skrev:

Så efter man deriverat så kan man utöver att identifiera MGN även förenkla bara en term i ekvationen genom 

Ja, det kan man och jag tror att du kan det. Det gäller också att vara lite förutseende - kommer det att göra enklare för mig, kan en annan term förenklas på samma sätt, blir hela uttrycket enklare efter det?

Men det är klart - man kan göra det.

Biorr skrev:

$x^2+3x-4=0$

Behöver du kvadratkomplettering?

Kvadratkomplettering  har vi för att du ska förstå varför man har pq-formeln. (Du kommer att behöva kvadratkomplettering på mattekurserna på högskolan, men det är några år tills dess)

$$\begin{gathered} f\text{'}\left(x\right)=0 \Rightarrow \frac{x^2}{3}+x-\frac{4}{3} = 0 \\ \Rightarrow x^2 + 3x - 4 = 0 \end{gathered}$$

Använd pq-formeln för ekvationen

Jag fick x₁ =1 och x₂ -4.

sedan gör man en teckentabell.

och sedan man in x-värden höger och vänster om x₁ och x₂ i den deriverade funktionen.

för att få en uppfattning om hur grafen ser ut.

+ så stiger grafen och - då sjunker grafen

Ja, sedan gör du en teckentabell (teckenstudie).

Där derivatan är + är funktionen växande och där derivatan är - är funktionen avtagande.

I punkterna där derivatan byter tecken är det en extrempunkt. Byter derivatan tecken från + till - är det en maximipunkt. Byter den tecken från - till +, är det en minimipunkt.