Derivera funktionsuttrycket

Börja med att skriva upp derivatans definition, och applicera den på den här funktionen.

Så här är min tankegång

Gör som Yngve brukar tipsa dig om: vad är f(5)? Vad är f(5+h)? Sätt in i derivatans definition.

Du har inte satt in korrekt i derivatans definition. Om du vill berökna f'(x) först i stället för att beräkna f'(5) direkt , borde uttrycket som man "gränsvärdar" vara $\frac{f(x+h)-f\left(x\right)}{h} = \frac{2{(x+h)}^2-3-(2x^2-3)}{h} = \frac{2(x^2+2xh+h^2)-3-2x^2+3}{h} =\hspace{0.17em}\frac{4xh+2h^2}{h}$. Du verkar ha tappat bort hela f(x) i täljaren.

Smaragdalena är det smidigast att beräkna f'(5) eller f'(x) ?

Arup skrev:

Smaragdalena är det smidigast att beräkna f'(5) eller f'(x) ?

Gör på båda sätten. Det är bra träning.

Men glöm inte "faktarutan".

Den ska I ena fallet innehålla

• ett uttryck för f(5) och ett uttryck för f(5+h)

och i andra fallet innehålla

• ett uttryck för f(x) och ett uttryck för f(x+h)

Gjorde jag inte fakta ruta när jag definierade T som 

$T=f(x+h)-f\left(x\right) ?$

Arup skrev:

Gjorde jag inte fakta ruta när jag definierade T som 

$T=f(x+h)-f\left(x\right) ?$

Nej. "faktarutan" består i detta fallet av två uttryck:

Ett uttryck för f(x) och ett uttryck för f(x+h).

Så här:

==== Faktaruta ====

• f(x) = 2x²-3
• f(x+h) = 2(x+h)²-3 = 2(x²+2xh+h²)-3 = 2x²+4xh+2h²-3

================

Fördelen med faktarutan är att vi kan skriva ut och förenkla de båda uttrycken vid sidan av, för att sedan kunna använda de färdigförenklade uttrycken i lösningen.

Vi slipper alltså att göra dessa operationer i ett mer komplicerat limes-uttryck.

Arup skrev:

Så här är min tankegång

Jag ser två fel:

1. Som Smaragdalena skrev sist i svar #4: Du har tappat bort termen f(x) i täljaren:

2. Den här förenklingen stämmer inte. Du har endast dividerat vissa av termerna I täljaren med h:

Ett till. Den här faktoriseringen stämmer inte:

Här får du förslag på en fullständig lösning.

Säg till om det är något/några av stegen som känns oklara.

Uppgift:

"Låt $f(x) = 2x^2-3$ och bestäm $f'(5)$ med hjälp av derivatans definition".

Lösningsförslag:

Derivatans definition ger oss att

$f'(5)=\lim_{h\rightarrow0}\frac{f(5+h)-f(5)}{h}=\lim_{h\rightarrow0}\frac{T}{h}$, där $T=f(5+h)-f(5)$.

Vi tar nu fram och förenklar ett uttryck för  $T$ med hjälp av följande "faktaruta":

========

Eftersom $f(x)=2x^2-3$ så är

• $f(5)=2\cdot5^2-3=2\cdot25-3=$

$=50-3=47$

• $f(5+h)=2\cdot(5+h)^2-3=$

$=2\cdot(5^2+2\cdot5\cdot h+h^2)-3=$

$=2\cdot(25+10h+h^2)-3=$

$=50+20h+2h^2-3=$

$=47+20h+2h^2$

===========

Det ger oss att

$T=f(5+h)-f(5)=$

$=47+20h+2h^2-47=$

$=20h+2h^2=h(20+2h)$

Nu kan vi sätta in detta uttryck för $T$ I derivatans definition:

$f'(5)=\lim_{h\rightarrow0}\frac{h(20+2h)}{h}=$

$=\lim_{h\rightarrow0}(20+2h)=20$

===========

Försök nu att på samma sätt ta fram ett uttryck för f'(x). 

för f'(x) kan vi väl ersätta 5 mot x 

Arup skrev:

för f'(x) kan vi väl ersätta 5 mot x 

Ja. Gör det!

Förstår du alla delar i mitt lösningsförslag?

Om nej, vilka delar vill du att vi förklarar närmare?

Om ja, försök gärna att härna lösningsförslaget så mycket det går när du jobbar fram ett uttryck för f'(x).

Tillägg: 2 aug 2024 11:38

Det ska stå härma, inte härna.

ja

Arup skrev:

ja

OK bra.

Visa ditt lösningsförslag om du vill ha återkoppling på det.

Yngve skrev:

Arup skrev:

ja

OK bra.

Visa ditt lösningsförslag om du vill ha återkoppling på det.

Är det så här du vill att jag ska lösa den ?

Snyggt!

Ja, det är så jag tycker att du ska ställa upp det. Det enda jag saknar är ett $\lim_{h\rightarrow0}$ innan det gulmarkerade uttrycket:

Yngve skrev:

Snyggt!

Ja, det är så jag tycker att du ska ställa upp det. Det enda jag saknar är ett $\lim_{h\rightarrow0}$ innan det gulmarkerade uttrycket:

Men jag har ju satt lim här :

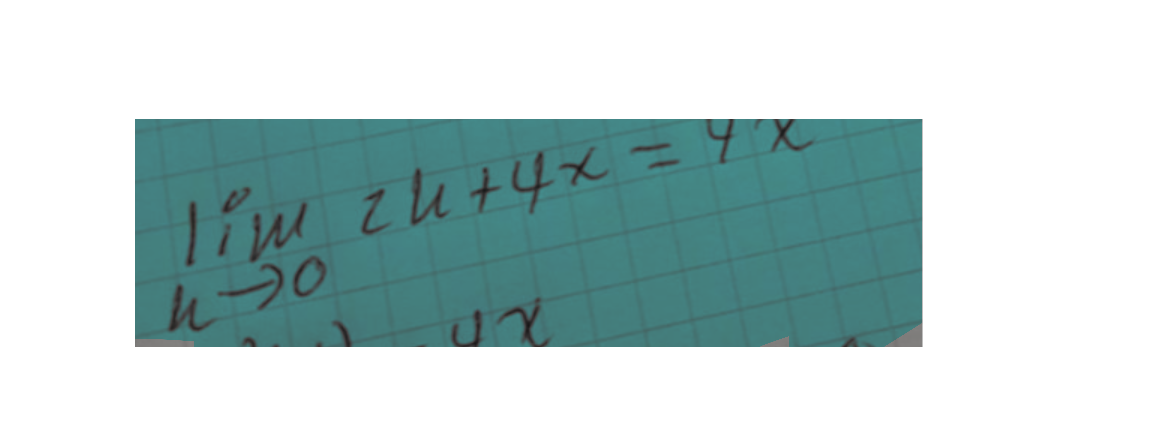
Det du skriver här:

är ett påstående som säger att $\lim_{h\rightarrow0}\frac{2h^2+4hx}{h}$ är identiskt med $2h+4x$.

Är det sant?

ja

Nej, det stämmer inte.

Du är väl med på att

$\lim_{h\rightarrow0}\frac{2h^2+4hx}{h}=$

$=\lim_{h\rightarrow0}\frac{h(2h+4x)}{h}=$

$=\lim_{h\rightarrow0}(2h+4x)=4x$?

Men samtidigt så säger du att $\lim_{h\rightarrow0}\frac{2h^2+4hx}{h}=2h+4x$

Det måste i så fall betyda att $4x=2h+4x$, vilket inte är sant.

Yngve kan du visa mig rätt lösning när jag skulle använt gränsvärdet ?

Arup skrev:

Yngve kan du visa mig rätt lösning när jag skulle använt gränsvärdet ?

Din lösning var jättebra, det enda du behöver göra är att byta ut det gulmarkerade mot $\lim_{h\rightarrow0}\frac{h(2h+4x)}{h}$.

är inte det samma sak eftersom om vi förenklar uttrycket får ju samma sav dvs 

$\underset{h\to 0}{\lim } 2h+4x$

Det Yngve menar är att du har missat att skiva $\underset{h\to 0}{\lim }$ före det förenklade uttrycket. I inlägg #25 har du skrivit rätt.

Vad får du om du förenklar $\underset{h\to 0}{\lim } 2h+4x$?

Arup skrev:

är inte det samma sak eftersom om vi förenklar uttrycket får ju samma sav dvs 

$\underset{h\to 0}{\lim } 2h+4x$

Nej, som jag skrev i svar #22 så är det inte samma sak.

Är du med på motiveringen i svar #22?

ja

Bra.

Är du då även med på att $\lim_{h\rightarrow0}\frac{2h^2+4hx}{h}$ inte är lika med $2h+4x$?

ok, då m¨åste vi väl bryta ut ett h ?

Arup skrev:

ok, då m¨åste vi väl bryta ut ett h ?

Innan vi fortsätter, är du verkligen med på det jag skrev I svar #29?

på sätt och vis är det för att vi inte kan dela täljaren med noll och därför måste vi bryta ut ett h ur uttrycket.

Nej det är inte därför.

Uttrycken är helt enkelt inte identiska, och det är därför fel att påstå att de är det, vilket du gör när du skriver ett likhetstecken mellan dem.

Jag försöker förtydliga:

Vi inför tre storheter $a$, $b$ och $c$ enligt följande:

• $a=\lim_{h\rightarrow0}\frac{2h^2+4hx}{h}$
• $b=4x$
• $c=2h+4x$

I och med dessa omskrivningar så kan vi prata om $a$, $b$ och $c$ istället för limes, h, nämnare och förenklingar.

I svar #22 har jag visat att $a=b$.

Vi vet att $b\neq c$.

Därför måste det gälla att $a\neq c$

Är du med på det resonemanget?

ja

OK bra.

Behöver du mer hjälp med något här?

Nej jag tror inte det