Derivatan av sin x och cos x
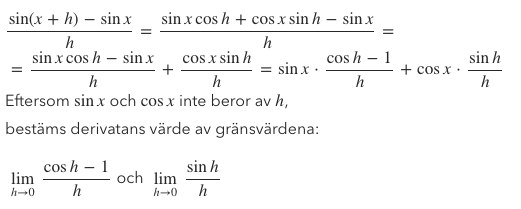
Jag förstår inte den andra förenklingen. Jag skulle vilja säga att HELA förenklingen av sin(x+h), dvs sin(x)cos(h)+cox(x)sin(h) ska tas subtraherat med sin(x), hur kan man bryta ut enbart den första termen sin(x)cos(h) och skriva att den ska subtraheras med sin(x)?
Study4life skrev:Jag skulle vilja säga att HELA förenklingen av sin(x+h), dvs sin(x)cos(h)+cox(x)sin(h) ska tas subtraherat med sin(x)
Detta är precis det de gör, efter det första =-tecknet.
Det de gör efter andra =-tecknet är att dela upp bråket i två delar, så att termerna i täljaren fördelas på två bråk, sin(x)*cos(h) och sin(x) som första bråkets täljare, och cos(x)*sin(h) som andra bråkets täljare.
Man skulle kunna skriva till bråken längst till höger på första raden, så kanske det blir tydligare?
Men borde det inte bli eftersom sin(x+h) är räknas som en term i sin helhet? Det går väl inte att dela upp den termen när HELA termen ska subtraheras med sin(x), dvs båda delarna;
del 1: sin(x)cos(h)
del 2: cos(x)sin(h)
Study4life skrev:Men borde det inte bli eftersom sin(x+h) är räknas som en term i sin helhet? Det går väl inte att dela upp den termen när HELA termen ska subtraheras med sin(x), dvs båda delarna;
del 1: sin(x)cos(h)
del 2: cos(x)sin(h)
Nej, varifrån fick du den andra temen "-sin(x)"? Förenkla ditt "högraste" uttryck!
Man får ändra på ordningen mellan termer som adderas och subtraheras, t ex a+b-c = a-c+b.
Ok, så om man får ändra hur som helst spelar det ingen roll att sin(x+h) är ETT uttryck varifrån sin(x) ska subtraheras ifrån, utan det delar upp sig och sedan kan man flytta termerna hel vilt?
Uttrycket sin(x+h) kan skrivas om till sin(x)cos(h)+cos(x)sin(h). Det är helt OK att skriva om ett uttryck till en summa med hjälp av additionsregeln för sinus.
Om du har tre termer, sin(x)cos(h), cos(x)sin(h) och -sin(x), så får du ordna dem i vilken ordning du vill.
Så sin(x)cos(h)+cos(x)sin(h) hänger alltså inte ihop efter uppdelningen?
Men om det skulle varit det omvänta: kan man ju inte bara ta -sin(x) för den ENA termen eftersom hela uttrycket sin(x)*cos(h)+cos(x)*sin(h) HÄNGER IHOP. Man kan ju inte dela upp det...
Varför inte? Även nu kan du skriva om sin(x+h) med hjälp av additionssatsen för sinus.
Men bordet inte tecknet ändras, precis som vilken annan subtraktion som helst. Dvs ????
Nu ser jag att jag inte la märke till hur konstigt du skrev. Om vi bara tar täljaren så blir det att
sinx-sin(x+h) = sinx-(sinxcosh+cosxsinh) = sinx-sinxcosh-cosxsinh = sinx(1-cosh)-cosxsinh.



