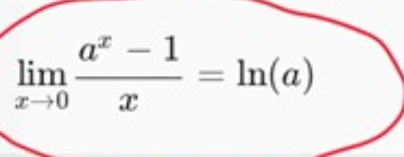Derivatan av n^x

Rad 1 är rätt.

Rad 2 är rätt.

På rad 3 tänker du nog rätt men skriver lite fel. Kan du hitta felet?

Men sista raden är rätt.

För att slutföra uträkningen behöver du veta vad gränsvärdet $\lim_{h\rightarrow0}\frac{n^h-1}{h}$ är.

Känner du till det?

Nej det gör jag inte

Förresten vad innebär ”standard gränsvärden” ?

Yngve jag vet inte vad jag gör för fel i rad 3. Jag bröt ju ut $n^x$

Arup skrev:

Yngve jag vet inte vad jag gör för fel i rad 3. Jag bröt ju ut $n^x$

Är verkligen det som står till vänster om likhetstecknet lika med det som står till höger?

Ja, eller vad har jag gjort för fel där ?

Arup skrev:

Förresten vad innebär ”standard gränsvärden” ?

Standardgränsvärde.

Arup skrev:

Ja, eller vad har jag gjort för fel där ?

Vi tar det steg för steg. Svara på följande frågor.

1. Hur ser f(x) ut? (Detta är första raden i faktarutan.)
2. Hur ser f(x+h) ut? (Detta är andra raden i faktarutan.)
3. Hur ser f(x+h)-f(x) ut? (Plocka från faktarutan.)

$$\begin{gathered} f\left(x\right)=n^x \\ f(x+h)=n^{x+h} \\ f(x+h)-f\left(x\right)= n^{x+h}-n^x \end{gathered}$$

Arup skrev:

$$\begin{gathered} f\left(x\right)=n^x \\ f(x+h)=n^{x+h} \\ f(x+h)-f\left(x\right)= n^{x+h}-n^x \end{gathered}$$

Ja, det stämmer. Ser du felet nu?

Nej tyvärr 

Kan du förgmarkera ?

De hör är ju rätt ?

Arup skrev:

De hör är ju rätt ?

Jag ser ingen bild.

Arup skrev:

Nej tyvärr 

Titta igen.

Vad står det till höger om likhetstecknet?

De här ju samma sak som i #12

Arup skrev:

De här ju samma sak som i #12

Nej, i #12 finns det ingen nämnare.

ok, men principen är väl rätt enigt derivatans definition:

$f\text{'}\left(x\right)=\underset{h\to 0}{\lim }\frac{f(x+h)-f\left(x\right)}{h}$

Ja, men det är inte det som står till vänster om likhetstecknet, där står det f(x+h) -f(x). Missbruk av likhetstecken är en mycket svår synd! ;-)

finns det nått bevi för det här ?

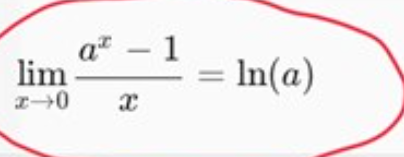
Ska det vara så här ?

$$\begin{gathered} f(x+h)-f\left(x\right)=n^{x+h}-n^x\Rightarrow n^x\times n^h-n^x \\ =n^x(n^h-1) \\ f\text{'}\left(x\right)=\underset{h\to 0}{\lim } \frac{n^x(n^h-1)}{h} \\ =\ln \left(n\right) \end{gathered}$$

Arup skrev:

finns det nått bevi för det här ?

Kolla Jonas Månssons video. Han visar att $\underset{x\to 0}{\lim }\frac{e^x-1}{x}=1$. Från det kan du sedan själv visa gränsvärdet ovan.

Arup skrev:

De här ju samma sak som i #12

Att du inte såg skillnad på detta

och detta

beror troligen på att din hjärna lurade dig att se vad du trodde att det stod, eller vad du ville att det skulle stå.

Det här är ett ganska vanligt problem som kan ställa till det rätt rejält, framför allt när det kommer till att kontrollera sina egna uträkningar.

Om du vill så kan jag ge dig ett tips på hur du kan minska risken att det händer igen. Säg till i så fall.

ja jag vill ha ett tips

OK, här kommer ett tips på en metod att kontrollera sina uträkningar.

Lägg ett papper över dina uträkningar.

Tänk i huvudet ut vad som borde stå på nästa rad i uträkningen, alternarivt skriv det på ett separat papper vid sidan av.

Dra sedan ner täckpapperet en liten bit och visa den rad i ursprungsuträkningen  som motsvarar den du nyss tänkte.ut/skrev ner.

Om de överensstämmer så var antingen båda uträkningarna rätt (troligast) eller båda uträkningarna fel på exakt samma sätt (mindre troligt).

Om de inte överensstämmer så är det sannolikt att det gömmer sig ett fel här.

Titta en extra gång på detta steg så att det verkligen blir rätt.

=======

En fördel med denna metod är att den tvingar en att göra små små tankesteg i uträkningarna och att skriva varje ny sak på en egen rad.

Bara detta sätt att skriva lösningar minskar risken för onödiga fel avsevärt.

Arup skrev:

Ska det vara så här ?

$$\begin{gathered} f(x+h)-f\left(x\right)=n^{x+h}-n^x\Rightarrow n^x\times n^h-n^x \\ =n^x(n^h-1) \\ f\text{'}\left(x\right)=\underset{h\to 0}{\lim } \frac{n^x(n^h-1)}{h} \\ =\ln \left(n\right) \end{gathered}$$

Nej, inte riktigt.

Det ska vara så här:

$f(x)=n^x$

$f(x+h)=n^{x+h}=n^x\cdot n^h$

$f(x+h)-f(x)=n^x\cdot n^h-n^x=$

$=n^x(n^h-1)$

$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}=$

$=\lim_{h\rightarrow0}\frac{n^x(n^h-1)}{h}=$

(Faktorn $n^x$ är oberoende av $h$ och kan därför "flyttas ut" ur gränsvärdesuttrycket)

$=n^x\cdot\lim_{h\rightarrow0}\frac{n^h-1}{h}=$

(Standardgränsvärde)

$=n^x\cdot\ln(n)$

varför kan man flytta $n^{x }$ur gränsvärde uttrycket ?

Du kan läsa mer om det t.ex. här.

ok, så gäller det bara för exponentiella funktioner ?

Nej, om det gäller generellt att

$\lim_{a\rightarrow b}(k\cdot c)=k\cdot\lim_{a\rightarrow b}$

om $k$ är konstant i sammanhanget, dvs om $a$ eller $c$ inte beror av $k$.

Tillägg: 3 aug 2024 16:21

Här blev det flera felskrivningar.

Det skulle stå

Det gäller generellt att 

$\lim_{a\rightarrow b}(k\cdot c)=k\cdot\lim_{a\rightarrow b}c$

om $k$$ är konstant (o.s.v)

Tillägg: 3 aug 2024 16:22

Suck.

... om $k$ är konstant (o.s.v)