Derivata & Tangent

Arup skrev:

Bestäm värdet på $a$så att grafen för $f\left(x\right)= 2x^2+x+a$ $$har $$en $$tangent.

med ekvationen $y=5x.$

Har du kommit till deriveringsregler än, eller måste du slita med derivatans definition?

sitta med derivatans definition

Vad är det för bok du har, som inte ser till att förse dig med de verktyg du behöver för att kunna lösa uppgifterna på ett effektivt sätt?

Arup skrev:

Bestäm värdet på $a$så att grafen för $f\left(x\right)= 2x^2+x+a$ $$har $$en $$tangent.

med ekvationen $y=5x.$

Uppgiften går att lösa utan att använda deriveringsregler, men det tar lite längre tid.

Känner du till sambandet mellan tangentens lutning och derivatans värde i tangeringspunkten?

nej

OK, vet du vad en tangent är?

Jag gjorde så hör, men får dessvärre inte fram ett uttryck för a.

Yngve skrev:

OK, vet du vad en tangent är?

Tangent är något som endast nuddar periferin endast en gång

Arup skrev:

Tangent är något som endast nuddar periferin endast en gång

Nästan.

En tangent kan skära en kurva på flera ställen.

Den kan även ha samma lutning som kurvan på flera ställen.

Det viktiga här är att en tangent är en rät linje som sammanfaller med en kurva vid en punkt som kallas tangeringspunkten och att tangentens lutning är samma som kurvans lutning i tangeringspunkten.

Om du klickar på länken i svar #6 så får du en tydlig beskrivning av vad en tangent är.

Arup skrev:

Jag gjorde så hör, men får dessvärre inte fram ett uttryck för a.

Här har det smugit sig in en extra h²-term (inringad i blått).

Den ska inte vara där. Men det är inte det som gör att du inte får rätt svar.

Oj, slarvfel. Men, jag ser inte om jag rättar felet hur jag får fram ett uttryck för a 

Här har du missat att skriva $\lim_{h\rightarrow0}$ (markerat i blått).

Men det är inte heller det som gör att du inte får rätt svar.

Här har du tappat bort ett h.(inringat i blått).

Det gör att din derivata blir fel.

Här behöver du inte använda gränsvärde.

Det anses vara välkänt att den räta linjen y = 5x har lutningen 5.

Yngve skrev:

Här behöver du inte använda gränsvärde.

Det anses vara välkänt att den räta linjen y = 5x har lutningen 5.

sant, men det skadar inte att träna derivatans definition.

Fortsättningen bör vara så här:

1. Ta fram ett korrekt uttryck för derivatan av f(x).
2. Ta reda på vid vilket x-värde som denna derivata har värdet 5.
3. Detta x-värde är nu x-koordinaten för tangeringspunkten. Det är viktigt att du förstår varför det blir så, se kommentar nedan om att rita grov skiss.
4. Beräkna y-koordinaten för tangeringspunkten.
5. Du kan nu anpassa värdet på konstanten a så att tangeringspunkten verkligen hamnar vid dessa koordinater.

Kommentar: Det kan vara en bra idé att rita en grov skiss av ett koordinatsystem, tangenten och parabeln.

Arup skrev:

sant, men det skadar inte att träna derivatans definition.

Det är sant. Och det var en snygg uträkning 👍

Jag förstår inte hur min skiss ska se ut. Kan du visa ?

Gå in på Desmos. Skriv in 5x och ENTER. Skriv in 2x^2+x+a på nästa rad och tryck på rutan märkt a. Då får du fram ett reglage så att du kan justera värdet på konstanten a så att det stämmer. Här är en bild där jag inte har ändrat defaultvärdet på a (som är a = 1).

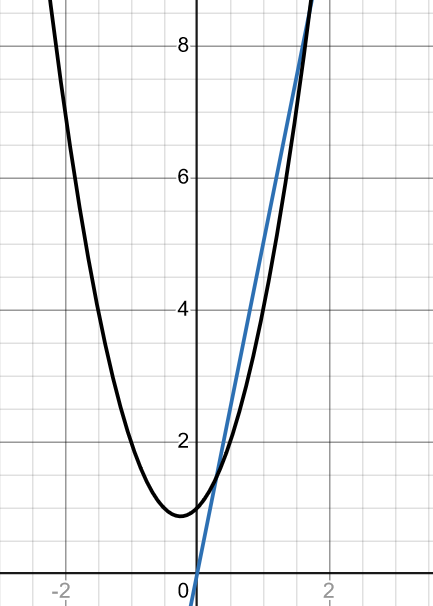
Det här är en bra kontroll av kunskaper om hur grafer beter sig.

Du ser i Smaragdalenas skiss att den räta linjen y = 5x skär parabeln på två ställen.

Du ser även att parabeln inte har samma lutning som linjen vid något av dessa ställen.

Linjen är alltså inte en tangent till parabeln.

Vi vill nu välja ett värde på konstanten a så att linjen blir en tangent till parabeln.

Kan du säga om konstanten a då ska ökas eller minskas?

OBS! Detta är inte en del av lösningen, men det är bra att träna upp förståelsen för hur parabelns placering påverkas av konstanten a.

Arup skrev:

Jag gjorde så hör, men får dessvärre inte fram ett uttryck för a.

Men, Yngve har jag anat faktarutan på rätt sätt ?

Nej, du har gjort samma fel som Yngve påpekade tidigare. Det gör att täljaren inte blir rätt.

Arup skrev:

Men, Yngve har jag anat faktarutan på rätt sätt ?

Vad menar du med "anat"?

oops jag tänkte skriva använt, men min keyboard skrev fel i förslagen

Arup skrev:

oops jag tänkte skriva använt, men min keyboard skrev fel i förslagen

OK, det är som sagt två fel i din beskrivning av f(x+h).

Du skriver f(x+h) = 2x²+4hx+3h²+x+a, men det ska vara f(x+h) = 2x²+4hx+2h²+x+h+a.

Se svar #11 och svar #14.

Yngve jag förstår inte hur jag kan ta mig vidare från punkt 2 i inlägg #17

Arup skrev:

Yngve jag förstår inte hur jag kan ta mig vidare från punkt 2 i inlägg #17

Derivatan är f'(x).

Du vill ta reda på när denna derivata har värdet 5.

Då ska du lösa ekvationen f'(x) = 5.