Derivata andragradspolynom
Hejsan! Behöver hjälp med denna uppgiften.
Tänkte först att funktionen är växande när x>-2 men inser att det inte är rätt. Hur ska man tänka på denna uppgift?! 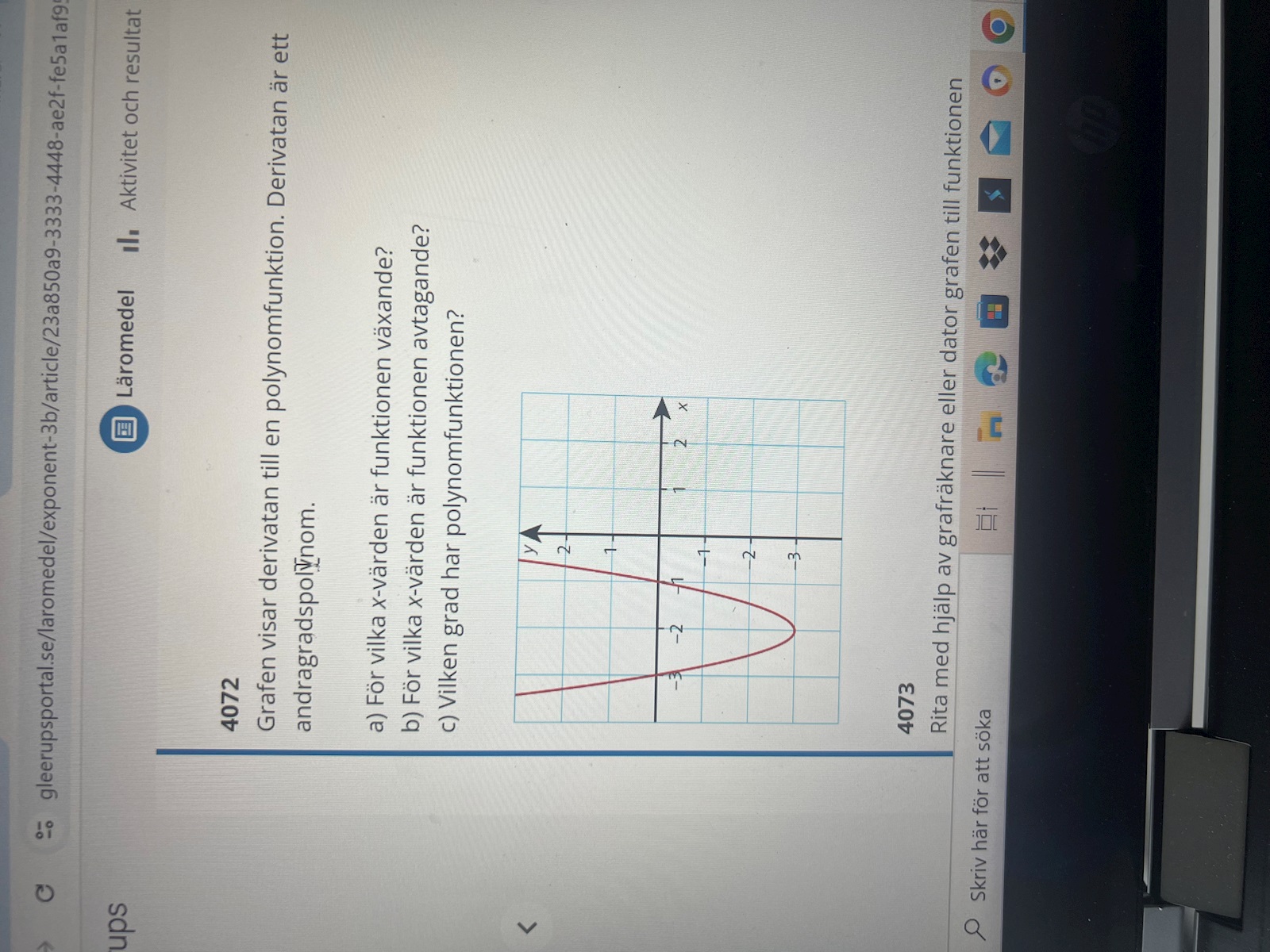
En funktion är växande om dess derivata är positiv, och avtagande om dess derivata är negativ.
Derivatan själv är växande för x > -2, och det betyder alltså att andraderivatan skulle vara positiv för x > -2.
Okej tack, men förstår inte hur svaret på a) kan bli x ≤ −3 och x ≥ −1 ? Måste man räkna andraderivatan eller något
Grafen visar derivatan av en funktion. Funktionen, som vi inte har en graf på, är växande när derivatan är positiv. För vilka värden är grafen på bilden, alltså derivatan, positiv?
Det är ju visst en graf till funktionen, vet bara inte hur man ska tänka när man ska läsa av den
Nej, grafen visar derivatan f'(x) av någon funktion f(x). Vi vet alltså inte hur f(x) ser ut. När jag säger 'funktion' menar jag alltså f(x). Derivatan f'(x) som visas i grafen är också en funktion, men det är inte den vi ska undersöka när den är växande eller avtagande, utan det är den ursprungliga funktionen f(x).
Vi vi att funktionen f(x) är växande när derivatan som visas i grafen är positiv. Tittar man på grafen ser man att den är positiv för x < -3 och x > -1. Mellan dessa x-värden är derivatan negativ, så där måste funktionen f(x) vara avtagande där.
Jaaha nu förstår jag vad du menar. Insåg inte att det var derivatan som visades utan trodde det var f(x). Då förstår jag att c) måste bli en tredje grad också :)

