Derivata

Derivata handlar i grunden om lutningen på en kurva eller graf i enskilda punkter. Vet du om vad k-värdet är? Kommer du ihåg hur man beräknar det? $k=\frac{∆y}{∆x}=\frac{skillnaden i y-led }{skillnaden i x-led}$För k-värde behöver du två punkter för att ta reda på en viss lutning. Detta gör du faktiskt med derivata också bara att dessa punkter är väldigt nära, rättare sagt oändligt nära varandra. Matematikens sätt för att göra att något kommer oändligt nära någonting annat är gränsvärden. 

Definitionen är således följande: 

Om vi har en funktion f(x) och ska beräkna k-värdet (lutningen) i en punkt så tar vi som vanligt $\frac{∆y}{∆x}$. Om vi kallar skillnaden i x-led ($∆x$) för h. Funktionsvärdet (y-värdet) i ena punkten vi använder är ju f(x). Den andra är h-steg bort, alltså kan dess funktionsvärde skrivas f(x+h). Skillnaden mellan dessa skrivs f(x+h)-f(x). Totalt blir då nästan k-värdet i en valfri punkt: $\frac{f(x+h)-f\left(x\right)}{h}$. h är som sagt skillnaden i x mellan dessa punkter. Om detta tal närmar sig 0 så minskar avståndet till oändligt litet (väldigt nära 0). För att uttrycka detta matematiskt skriver vi: 

$f\text{'}\left(x\right)=\underset{h\to 0}{\lim }\frac{f(x+h)-f\left(x\right)}{h}$

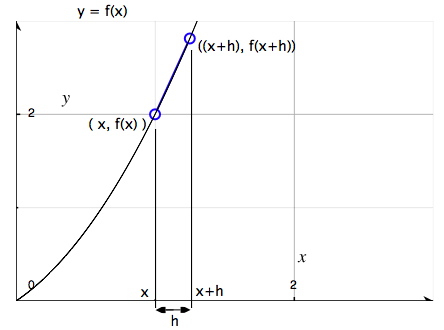
Mrpotatohead skrev:

Derivata handlar i grunden om lutningen på en kurva eller graf i enskilda punkter. Vet du om vad k-värdet är? Kommer du ihåg hur man beräknar det? $k=\frac{∆y}{∆x}=\frac{skillnaden i y-led }{skillnaden i x-led}$För k-värde behöver du två punkter för att ta reda på en viss lutning. Detta gör du faktiskt med derivata också bara att dessa punkter är väldigt nära, rättare sagt oändligt nära varandra. Matematikens sätt för att göra att något kommer oändligt nära någonting annat är gränsvärden. 

Definitionen är således följande: 

Om vi har en funktion f(x) och ska beräkna k-värdet (lutningen) i en punkt så tar vi som vanligt $\frac{∆y}{∆x}$. Om vi kallar skillnaden i x-led ($∆x$) för h. Funktionsvärdet (y-värdet) i ena punkten vi jämför är ju f(x). Den andra är h-steg bort, alltså kan dess funktionsvärde skrivas f(x+h). Skillnaden mellan dessa skrivs f(x+h)-f(x). Totalt blir då nästan k-värdet i en valfri punkt: $\frac{f(x+h)-f\left(x\right)}{h}$h är som sagt skillnaden i x mellan dessa punkter. Om detta tal närmar sig 0 så minskar avståndet till oändligt litet (väldigt nära 0). För att uttrycka detta matematiskt skriver vi: 

$f\text{'}\left(x\right)=\underset{h\to 0}{\lim }\frac{f(x+h)-f\left(x\right)}{h}$

Wow tack så mycket!!

Detta gav faktiskt mig en helt annan inblick i hela derivata-världen jämfört med vad jag tidigare läst. Nu ska jag försöka igen!

Vad bra. Kör på och lycka till!

intressant!

Arup skrev:

intressant!

Verkligen!

Vad är meningen med att derivera saker ?

Arup skrev:

Vad är meningen med att derivera saker ?

Att undersöka hur någonting förändras.

Smaragdalena skrev:

Arup skrev:

Vad är meningen med att derivera saker ?

Att undersöka hur någonting förändras.

Jag förstår inte riktigt den praktiska meningen med derivata varför vill man se hur t ex uttrycket $3x^2+5x+6$ förändras ? 

Om din funktion beskriver en förändring i praktiken över exempelvis en viss tid. Då kan derivatan användas till ta reda på förändringen i en tidpunkt. 

Om funktionen beskriver t ex hur en bakteriepopulation varierar (förändras) över tiden,
så anger derivatan populationens förändringstakt vid varje tidpunkt.
Dess graf visar därför hur förändringstakten varierar över tiden.

Parabeln i ditt exempel visar hur y-värdet varierar (förändras) över tiden.
Derivatan visar hur brant funktionsgrafen är och hur "brantheten" varierar. 
När derivatan är lika med noll har parabeln ett extremvärde (max el min).
Det kan ofta vara bra att veta :-). Derivatan visar var det händer.

Om du har en funktion f(t) som beskriver var ett föremål är och deriverar funktionen, får du en funktion som beskriver föremålets hastighet. Om du deriverar en gång till får du föremålets acceleratoin. Om du deriverar en tredje gång får du derivatans förändring (detta kallas ibland ryck, och det är ett väldigt bra namn!).

Arup skrev:

Vad är meningen med att derivera saker ?

Skapa gärna en egen tråd med dina frågor kring derivata.