Delbarhet för alla heltal n: Hur är dessa uttryck ekvivalenta?
Hej!
Har följande uppgift med tillhörande facit:
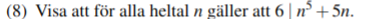
Facit:
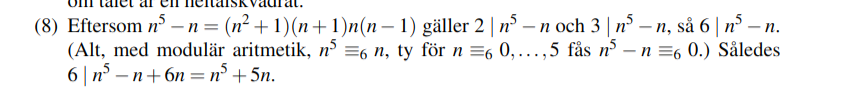
Jag förstår inte riktigt vad man gör i facit, på någon av stegen (alternativet och "det vanliga").
Det första jag inte riktigt förstår, är varför man undersöker och inte . Sedan förstår jag ändå inte hur man utifrån att vi kan faktorisera uttrycket, kan avgöra att 2 och 3 är faktoriseringar av uttrycket?
(modulär aritmetik-lösningen känner jag att jag klickar mycket mer med om jag kan förstå varför man använt ).
Som vanligt enormt tacksam för all hjälp!
n-1, n och n+1 är tre på varandra följande heltal, så något av dem måste vara delbart med 3, och minst ett av dem måste vara delbart med 2.
På något sätt har man kommit på att det ger mer att faktorisera n5-n än n5+5n.
Den alternativa lösningen behöver inte den insikten, det går bra med det ursprungliga uttrycket.
Laguna skrev:n-1, n och n+1 är tre på varandra följande heltal, så något av dem måste vara delbart med 3, och minst ett av dem måste vara delbart med 2.
På något sätt har man kommit på att det ger mer att faktorisera n5-n än n5+5n.
Den alternativa lösningen behöver inte den insikten, det går bra med det ursprungliga uttrycket.
Aha, yes, tack!Då tror jag att den alternativa lösningen är bättre. Nu behöver jag bara se att jag förstår mig på den också!Hur kan vi se att ? Eller bygger det på nästa insikt, att för gäller ? Jag tänker mig att det är just "nästa insikt" som är det man ska bevisa, och här känns det bara som att de skrivit ut det som om det vore ett faktum. Eller är det helt enkelt att man testar alla och ser att det stämmer?
coffeshot skrev:Laguna skrev:n-1, n och n+1 är tre på varandra följande heltal, så något av dem måste vara delbart med 3, och minst ett av dem måste vara delbart med 2.
På något sätt har man kommit på att det ger mer att faktorisera n5-n än n5+5n.
Den alternativa lösningen behöver inte den insikten, det går bra med det ursprungliga uttrycket.
Aha, yes, tack!Då tror jag att den alternativa lösningen är bättre. Nu behöver jag bara se att jag förstår mig på den också!Hur kan vi se att ? Eller bygger det på nästa insikt, att för gäller ? Jag tänker mig att det är just "nästa insikt" som är det man ska bevisa, och här känns det bara som att de skrivit ut det som om det vore ett faktum. Eller är det helt enkelt att man testar alla och ser att det stämmer?
Ja, man beräknar helt enkelt för och ser att samtliga tal är delbara med 6. Således kan man dra slutsatsen att mod 6. Det "snyggare" sättet är dock att faktorisera och argumentera för att produkten av tre på varandra följande heltal måste vara delbar med 6.
Tack, nu hänger jag med!



