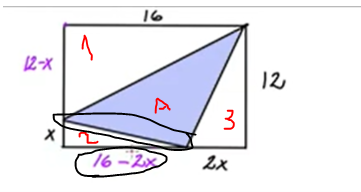
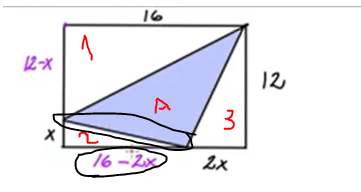
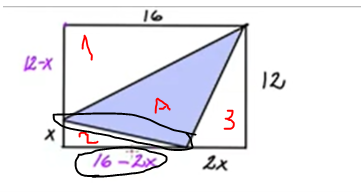
defintionsmängd för A
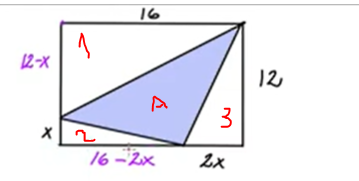
jag vill få ut definitionsmängden för A.
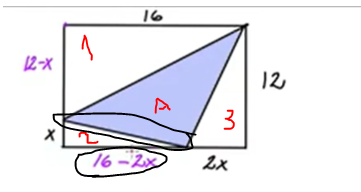
area 1: 96-8x
area 2: 8x-x2
area 3: 12x
area A: 96- 12x + x2
kan någon hjälpa mig på traven?
Vet du vad definitionsmängd innebär? Vad frågar de efter?
mrpotatohead skrev:Vet du vad definitionsmängd innebär? Vad frågar de efter?
vilka x-värden som är möjliga
naturnatur1 skrev:mrpotatohead skrev:Vet du vad definitionsmängd innebär? Vad frågar de efter?
vilka x-värden som är möjliga
Ja, precis och vilka x är möjliga?
Visa spoiler
Det enda du behöver ta hänsyn här är att det är sträckor vi tittar på, vilket betyder att vi inte kan ha negativa värden.
mrpotatohead skrev:naturnatur1 skrev:mrpotatohead skrev:Vet du vad definitionsmängd innebär? Vad frågar de efter?
vilka x-värden som är möjliga
Ja, precis och vilka x är möjliga?
Visa spoiler
Det enda du behöver ta hänsyn här är att det är sträckor vi tittar på, vilket betyder att vi inte kan ha negativa värden.
jag tänkte 0 < x < 12
men det var tydligen fel?
Ja justde ja, haha oj, det har du självklart rätt i. Det stämmer bra det;)
mrpotatohead skrev:Ja justde ja, haha oj, det har du självklart rätt i. Det stämmer bra det;)
vad menar du?
jag förstår inte riktigt hur man kommer fram till korrekt definitionsmängd:/
Helt enkelt kolla på figuren. 12-x får ju inte vara större än 12 eller mindre än 0.
Kan uttryckas i olikheterna:
12-x<12
12-x>0
Om du löser och kombinerar dessa så får du 0<x<12.
mrpotatohead skrev:Helt enkelt kolla på figuren. 12-x får ju inte vara större än 12 eller mindre än 0.
Kan uttryckas i olikheterna:
12-x<12
12-x>0
Om du löser och kombinerar dessa så får du 0<x<12.
jo, men jag tänkte typ också så. men det är tydligen fel
rätt svar är 0 < x < 8
Justde, ber om ursäkt igen
Du behöver självklart göra samma sak med långsidan.
mrpotatohead skrev:Justde, ber om ursäkt igen
Du behöver självklart göra samma sak med långsidan.
ingen fara, detta råka nog bara bli den tionde tråden, hahah(:
men jag förstår inte riktigt "principen" bakom och hur man kommer fram till det
varför är 0 < x < 12 fel?
och hur vet man att dessa sträckor är lika?
den vid triangeln kanske har andra mått?
naturnatur1 skrev:mrpotatohead skrev:Justde, ber om ursäkt igen
Du behöver självklart göra samma sak med långsidan.
ingen fara, detta råka nog bara bli den tionde tråden, hahah(:
:) (jag lär mig mer av att försöka hjälpa alla än eleverna jag hjälper..)
men jag förstår inte riktigt "principen" bakom och hur man kommer fram till det
varför är 0 < x < 12 fel?
och hur vet man att dessa sträckor är lika?
Det gör man inte. Varför tror du det?
den vid triangeln kanske har andra mått?
Du ser ju att både lång- och kortsidan har fasta mått.
Egentligen, nu när jag tänker på det så kan man bara tänka på vilken del av sidorna som kan variera:
Kortsidan har x som man bara genom att kolla på andra sidan kortsidan inte får vara mindre än 0 eller större än 12.
Långsidan har 2x. 2x får inte vara större än 16 eller mindre än 0. Vilket ger 0<x<8. Om du kombinerar intervallen så får man bara 0<x<8 kvar eftersom x:et ska tillhöra BÅDA inte enbart ett.
mrpotatohead skrev:naturnatur1 skrev:mrpotatohead skrev:Justde, ber om ursäkt igen
Du behöver självklart göra samma sak med långsidan.
ingen fara, detta råka nog bara bli den tionde tråden, hahah(:
:) (jag lär mig mer av att försöka hjälpa alla än eleverna jag hjälper..)
men jag förstår inte riktigt "principen" bakom och hur man kommer fram till det
varför är 0 < x < 12 fel?
och hur vet man att dessa sträckor är lika?
Det gör man inte. Varför tror du det?
för det är ju den delen av rektangelns sida som är 16-2x
men det är den blåa triangelns area man efterfrågar, men trots det har man använt rektangelns?
(alltså fått fram 8:an därifrån)
den vid triangeln kanske har andra mått?
Du ser ju att både lång- och kortsidan har fasta mått.
Egentligen, nu när jag tänker på det så kan man bara tänka på vilken del av sidorna som kan variera:
Kortsidan har x som man bara genom att kolla på andra sidan kortsidan inte får vara mindre än 0 eller större än 12.
Långsidan har 2x. 2x får inte vara större än 16 eller mindre än 0. Vilket ger 0<x<8. Om du kombinerar intervallen så får man bara 0<x<8 kvar eftersom x:et ska tillhöra BÅDA inte enbart ett.
hänger inte riktigt med om jag ska va ärlig, skulle du kunna förtydliga? tack på förhand
naturnatur1 skrev:mrpotatohead skrev:naturnatur1 skrev:mrpotatohead skrev:Justde, ber om ursäkt igen
Du behöver självklart göra samma sak med långsidan.
ingen fara, detta råka nog bara bli den tionde tråden, hahah(:
:) (jag lär mig mer av att försöka hjälpa alla än eleverna jag hjälper..)
men jag förstår inte riktigt "principen" bakom och hur man kommer fram till det
varför är 0 < x < 12 fel?
och hur vet man att dessa sträckor är lika?
Det gör man inte. Varför tror du det?
för det är ju den delen av rektangelns sida som är 16-2x
men det är den blåa triangelns area man efterfrågar, men trots det har man använt rektangelns?
(alltså fått fram 8:an därifrån)
Ja men A:s definitionsmängd beror ju på vad x får vara. Och x beror på figurens storlek.
den vid triangeln kanske har andra mått?
Du ser ju att både lång- och kortsidan har fasta mått.
Egentligen, nu när jag tänker på det så kan man bara tänka på vilken del av sidorna som kan variera:
Kortsidan har x som man bara genom att kolla på andra sidan kortsidan inte får vara mindre än 0 eller större än 12.
Långsidan har 2x. 2x får inte vara större än 16 eller mindre än 0. Vilket ger 0<x<8. Om du kombinerar intervallen så får man bara 0<x<8 kvar eftersom x:et ska tillhöra BÅDA inte enbart ett.
hänger inte riktigt med om jag ska va ärlig, skulle du kunna förtydliga? tack på förhand
Okej. Kolla inte för hårt på figuren eftersom den kan förändras beroende på x. Förstår du att triangelns nedre hörn kan flyttas hursomhelst över sidorna beroende på x?
X får alltså variera men det kan ju inte variera hur mycket som helst, utan x får, eller rättare sagt kan, bara vara värden som först om främst är positiva (finns inte negativa sträckor) och som inte gör att figuren inte längre är en rektangel. Dvs, motstående sidor ska vara lika långa.