Definitionsmängden och största möjliga volym
Hej! Skulle behöva hjälp med b och c frågan. 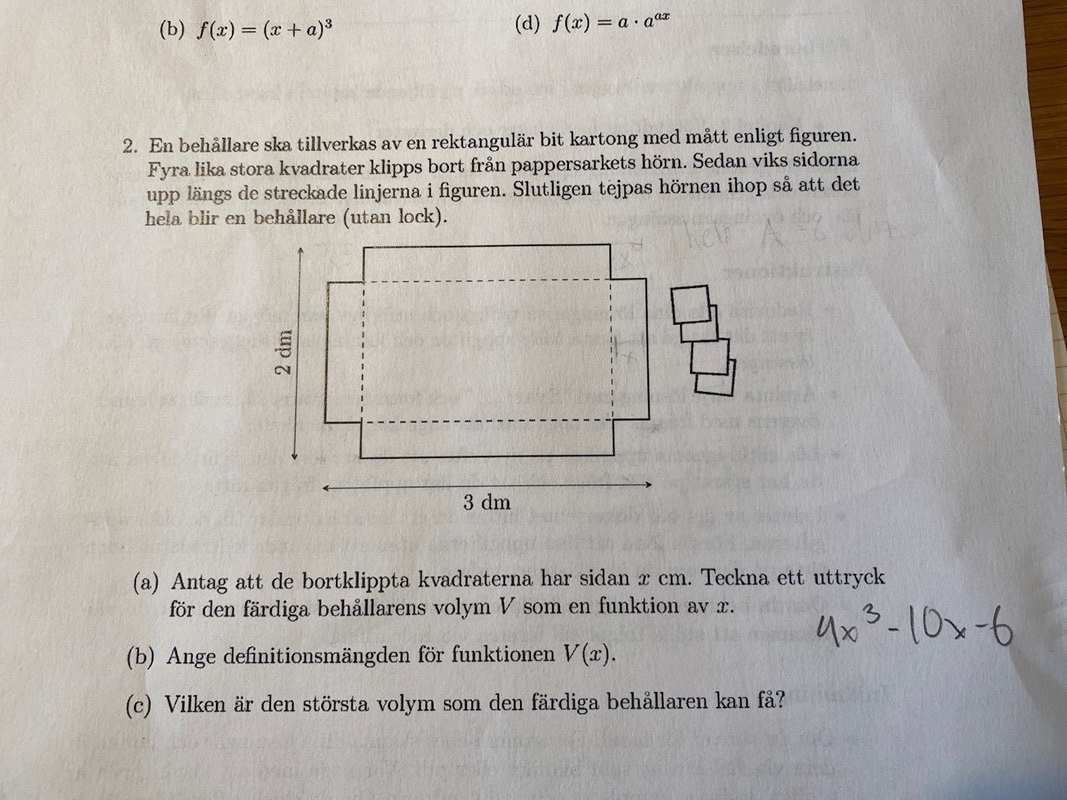
Vad är ditt svar på a?
Fundera på vad den maximala storleken på hörnen man klipper ut kan vara.
mrpotatohead skrev:Vad är ditt svar på a?
Fundera på vad den maximala storleken på hörnen man klipper ut kan vara.
4x3-10x2-6x.
Behöver jag derivera för att ta reda på den maximala storleken på hörnen?
LinneaL skrev:mrpotatohead skrev:Vad är ditt svar på a?
Fundera på vad den maximala storleken på hörnen man klipper ut kan vara.
4x3-10x2-6x.
Kan tyvärr inte kontrollräkna nu men det ska vara:
V(x) = (3-2x)(2-2x)x
Behöver jag derivera för att ta reda på den maximala storleken på hörnen?
Ingen dimension (bas, höjd eller djup) får vara negativ. Där är den inte definierad, således dess definitionsmängd.
Vilka x hade gjort att (3-2x), (2-2x) eller x blir negativt?
mrpotatohead skrev:LinneaL skrev:mrpotatohead skrev:Vad är ditt svar på a?
Fundera på vad den maximala storleken på hörnen man klipper ut kan vara.
4x3-10x2-6x.
Kan tyvärr inte kontrollräkna nu men det ska vara:
V(x) = (3-2x)(2-2x)x
Behöver jag derivera för att ta reda på den maximala storleken på hörnen?
Ingen dimension (bas, höjd eller djup) får vara negativ. Där är den inte definierad, således dess definitionsmängd.
Vilka x hade gjort att (3-2x), (2-2x) eller x blir negativt?
Vad är det du brutit ut för att få (3-2x) och (2-2x)?
Inte brutit ut något. För att räkna ut volymen tar man basen*höjden*längden.
Basen kan uttryckas 3 dm minus det man klippt bort (x+x=2x), dvs 3-2x.
Samma resonemang för längden.
Höjden är x.
mrpotatohead skrev:Inte brutit ut något. För att räkna ut volymen tar man basen*höjden*längden.
Basen kan uttryckas 3 dm minus det man klippt bort (x+x=2x), dvs 3-2x.
Samma resonemang för längden.
Höjden är x.
Okej, då hänger jag med.
Hur ska jag tänka i c) frågan. Ska jag först derivera funktionen och sedan ta fram nollställerna?


