Definitionsmängd/värdemängd av sammansatta funktioner

Med sammansatta funktioner menar man i regler funktioner av funktioner, men jag tror att du menar för vilka reella x- och y är funktionerna definierade.

Logaritmfunktionen $\ln(t)$ är definierad för alla t större än noll. Alltså är $ln(2x-2y-4)$ definierad för alla x och y så att $2x-2y-4>0$ (vilket ger dig ett område och en begränsningslinje i planet), vidare är $\sqrt t$ definierad för alla t större än eller lika med noll, alltså är $\sqrt{16-x^2-y^2}$ definierad för alla x- och y sådana att $x^2+y^2\leq 16$ (en cirkel med radie 4). Slutligen är $x/t$ definierad för alla x och t sådana att $t\neq 0$. Dvs det som står under rottecknet måste vara skilt från noll.

Sätter man ihop all information och tar snittet av mängderna får man den största möjliga definitionsmängden för uttrycket.

Tack för förtydligandet! Just hur man sätter ihop all denna ihop och sedan ritar är det jag inte riktigt förstår. Vill du förklara hur du skulle ha gjort i detta fall?

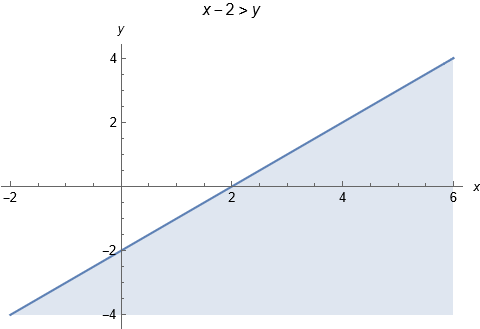
Om vi t.ex. tar uttrycket för logaritmfunktionen så måste argumentet vara strikt större än 0.

$2x-2y-4\gt 0$

Om vi adderar 2y på båda sidor om likhetstecknet får vi

$2x-4\gt 2y$

Vi kan också dela båda sidor med ett positiva talet 2 utan att det händer något underligt med olikheten:

$x-2\gt y$

Vid likhet blir detta en linje, och uttrycket är uppfyllt för alla de x och y som ligger under linjen, vi ritar linjen och markerar med blå färg det område för vilka olikheten gäller i en graf:

Jag är kanske otydlig. :)

Hela uttrycket är ju ln(2x-2y-4)+x/sqrt(16-x^2-y^2). Visserligen måste 2x-2y-4> 0. Och sqrt(16-x^2-y^2)=>0 samt inte vara lika med 0 då uttrycket är i nämnaren.

Min fråga är: hur tillfredsställer jag samtliga villkor ovan för att ta reda på vad x och y får vara, samt hur ritar jag det definierade området i en graf?

Fortsätt arbetet som D4NIEL påbörjade.

1. Beskriv algebraiskt alla viklkor som måste vara uppfyllda. Det blir en olikhet för varje villkor.
2. Illustrera dessa olikheter i ett och samma koordinatsystem. Det blir ett område för varje olikhet.

Definitionsmängden kommer sedan att vara skärningen mellan alla dessa områden.